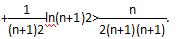题目内容
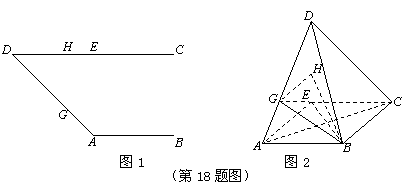
如图1,直角梯形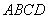 中,
中,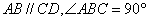 ,
,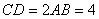 ,
, .
.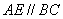 交
交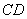 于点
于点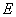 ,点
,点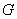 ,
,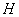 分别在线段
分别在线段 ,
, 上,且
上,且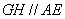 . 将图1中的
. 将图1中的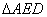 沿
沿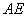 翻折,使平面
翻折,使平面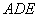 ⊥平面
⊥平面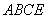 (如图2所示),连结
(如图2所示),连结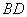 、
、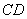 ,
,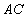 、
、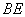 .
.
(Ⅰ)求证:平面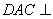 平面
平面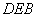 ;
;
 (Ⅱ)当三棱锥
(Ⅱ)当三棱锥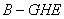 的体积最大时,求直线
的体积最大时,求直线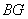 与平面
与平面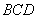 所成角的正弦值.
所成角的正弦值.
解:(Ⅰ)∵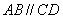 ,
,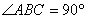 ,
,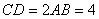
又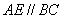 交
交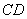 于点
于点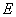 .
.
∴四边形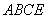 是边长为2的正方形 ………………………1分
是边长为2的正方形 ………………………1分
∴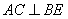 ,
, .
.
又∵平面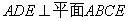
平面
∴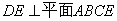 ………………………3分
………………………3分
∵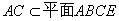 ,∴
,∴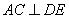 ……………………4分
……………………4分
又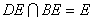
∴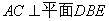 ………………………5分
………………………5分
∵
∴平面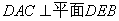 ………………………6分
………………………6分
(Ⅱ)由(Ⅰ)知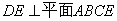 ,
,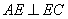
以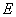 为原点,
为原点,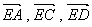 的方向为
的方向为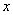 轴,
轴,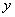 轴,
轴, 轴的正方向建立空间直角坐标系. ………………………7分
轴的正方向建立空间直角坐标系. ………………………7分
则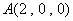 ,
,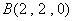 ,
,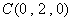 ,
,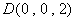
设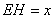 ,则
,则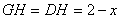 (
(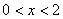 )
)
∵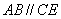 ,∴
,∴ …………………8分
…………………8分
∴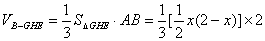
 ………………………9分
………………………9分
∵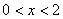 ,∴
,∴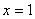 时,三棱锥
时,三棱锥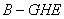 体积最大,此时,
体积最大,此时,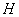 为
为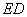 中点.
中点.
∵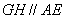 ,∴
,∴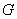 也是
也是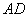 的中点,∴
的中点,∴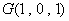 ,
,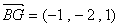 .…10分
.…10分
设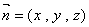 是面
是面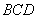 的法向量.
的法向量.
则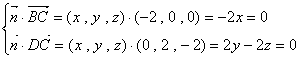
令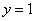 ,得
,得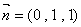 ………………………11分
………………………11分
设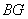 与面
与面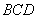 所成角为
所成角为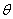
则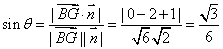
∴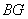 与平面
与平面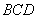 所成角的正弦值为
所成角的正弦值为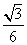 . ………………………13分
. ………………………13分

练习册系列答案
相关题目
 与直线x=1,x=4及x轴所围成的区域的面积是( )
与直线x=1,x=4及x轴所围成的区域的面积是( ) B.ln2 C.2ln2 D.ln2-2
B.ln2 C.2ln2 D.ln2-2 的展开式中各
的展开式中各 项二项式系数和是16,则展开式中的常数项是____.
项二项式系数和是16,则展开式中的常数项是____.
 表示的平面区域为
表示的平面区域为 ,不等式
,不等式 表示的平面区域为
表示的平面区域为 .现随机向区域
.现随机向区域 .
. ,求
,求 的最大值.
的最大值.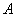 、
、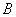 、
、 满足
满足 ,
, ,
, ,则
,则

 的值等于
的值等于 B.
B. C.
C. D.
D.
 ,
, 的夹角为
的夹角为 ,且
,且 ,
, ,则
,则 ( )
( )  B.
B. C.
C. D.
D.
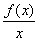 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;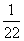 ln22+
ln22+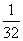 ln32+
ln32+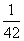 ln42+…
ln42+…