题目内容
若{x|x2+mx-8=0}={-2,n},则m+n= .
考点:集合的相等
专题:集合
分析:利用集合相等、一元二次方程的根与系数的关系即可得出.
解答:
解:∵{x|x2+mx-8=0}={-2,n},
∴-2,n是一元二次方程x2+mx-8=0的两个实数根,
∴-2+n=-m,-2n=-8,
解得n=4,m=-2.
∴m+n=2.
故答案为:2.
∴-2,n是一元二次方程x2+mx-8=0的两个实数根,
∴-2+n=-m,-2n=-8,
解得n=4,m=-2.
∴m+n=2.
故答案为:2.
点评:本题考查了集合相等、一元二次方程的根与系数的关系,属于基础题.

练习册系列答案
相关题目
如图所示程序框图,那么输出的数是( )


| A、5050 | B、4900 |
| C、2550 | D、2450 |
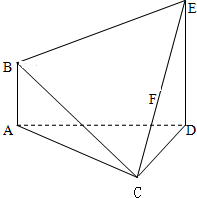 如图所示的多面体ABEDC中,AB⊥平面ACD,DE⊥平面ACD,且AC=CD,DE=2AB=2,AC=CD=7,AD=7,求多面体ABEDC的体积.
如图所示的多面体ABEDC中,AB⊥平面ACD,DE⊥平面ACD,且AC=CD,DE=2AB=2,AC=CD=7,AD=7,求多面体ABEDC的体积.