题目内容
13.对定义域分别是Df,Dg的函数f(x)和g(x),有如下定义函数$h(x)=\left\{{\begin{array}{l}{f(x)g(x),x∈{D_f}且x∈{D_g}}\\{f(x),x∈{D_f}且x∉{D_g}}\\{g(x),x∉{D_f}且x∈{D_g}}\end{array}}\right.$(1)若函数$f(x)=\frac{1}{x+1},g(x)={x^2}$,写出h(x)的解析式;
(2)在(1)的条件下,证明函数h(x)在(0,1)上的单调性.
分析 (1)直接根据题中新定义分三类求函数的解析式;
(2)运用单调性的定义,即利用作差比较法证明函数的单调性.
解答 解:(1)因为$f(x)=\frac{1}{x+1},g(x)={x^2}$,
所以,Df=(-∞,-1)∪(-1,+∞),Dg=(-∞,+∞),
根据h(x)的定义,分三类讨论如下:
①当x∈Df且x∈Dg,得x∈(-∞,-1)∪(-1,+∞),此时,h(x)=f(x)g(x)=$\frac{x^2}{x+1}$;
②当x∈Df且x∉Dg,得x∈∅;
③当x∉Df且x∈Dg,得x=-1,此时,h(x)=g(x)=x2=1,
综合以上讨论得,h(x)=$\left\{\begin{array}{l}{\frac{x^2}{x+1},x≠-1}\\{1,x=-1}\end{array}\right.$;
(2)当x∈(0,1)时,h(x)=$\frac{x^2}{x+1}$,
任取x1,x2∈(0,1),且x1<x2,
则$h({x_1})-h({x_2})=\frac{x_1^2}{{{x_1}+1}}-\frac{x_2^2}{{{x_2}+1}}$
=$\frac{{x_1^2{x_2}+x_1^2-x_2^2{x_1}-x_2^2}}{{({{x_1}+1})({{x_2}+1})}}=\frac{{{x_1}{x_2}({{x_1}-{x_2}})+({{x_1}-{x_2}})({{x_1}+{x_2}})}}{{({{x_1}+1})({{x_2}+1})}}$
=$\frac{{({{x_1}-{x_2}})({{x_1}{x_2}+{x_1}+{x_2}})}}{{({{x_1}+1})({{x_2}+1})}}$,
由于(x1+1)(x2+1)>0,x1x2+x1+x2>0,x1-x2<0,
故h(x1)-h(x2)<0,即h(x1)<h(x2),
由函数单调性的定义可知,h(x)在(0,1)上单调递增.
点评 本题主要考查了函数解析式的求法,以及分段函数的表示,并用作差比较法证明函数的单调性,属于中档题.

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案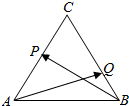 如图,在△ABC中,已知$\overrightarrow{AP}$=$\overrightarrow{PC}$,$\overrightarrow{CQ}$=2$\overrightarrow{QB}$,设$\overrightarrow{BP}$=m•$\overrightarrow{AB}$+n•$\overrightarrow{AC}$.
如图,在△ABC中,已知$\overrightarrow{AP}$=$\overrightarrow{PC}$,$\overrightarrow{CQ}$=2$\overrightarrow{QB}$,设$\overrightarrow{BP}$=m•$\overrightarrow{AB}$+n•$\overrightarrow{AC}$.