题目内容
3.已知数列{an}中,a1=1,Sn为数列{an}的前n项和,且当n≥2时,有$\frac{2{a}_{n}}{{a}_{n}{S}_{n}-{{S}^{2}}_{n}}$=1成立,则S2017=$\frac{1}{1009}$.分析 当n≥2时,有$\frac{2{a}_{n}}{{a}_{n}{S}_{n}-{{S}^{2}}_{n}}$=1成立,可得2(Sn-Sn-1)=(Sn-Sn-1)Sn-${S}_{n}^{2}$,化为:$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$=$\frac{1}{2}$,利用等差数列的通项公式即可得出.
解答 解:∵当n≥2时,有$\frac{2{a}_{n}}{{a}_{n}{S}_{n}-{{S}^{2}}_{n}}$=1成立,∴2(Sn-Sn-1)=(Sn-Sn-1)Sn-${S}_{n}^{2}$,化为:$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$=$\frac{1}{2}$,
∴数列$\{\frac{1}{{S}_{n}}\}$是等差数列,公差为$\frac{1}{2}$,首项为1.
∴$\frac{1}{{S}_{n}}$=1+$\frac{1}{2}$(n-1)=$\frac{n+1}{2}$,解得Sn=$\frac{2}{n+1}$.
∴S2017=$\frac{2}{2018}$=$\frac{1}{1009}$.
故答案为:$\frac{1}{1009}$.
点评 本题考查了数列递推关系、等差数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
13.已知$a=\frac{1}{π}\int_{-1}^1{(\sqrt{1-{x^2}}+sinx)dx}$,则二项式${(2x-\frac{a}{x^2})^9}$的展开式中的常数项为-672.
14.为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,如表记录了小李某月1号到5号每天打篮球的时间x(单位:小时)与当天投篮命中率y之间的关系:
(Ⅰ)求小李这5天的平均投篮命中率
(Ⅱ)用线性回归分析方法,预测小李该月6号打3.5小时篮球的投篮命中率(保留2位小数点)
参考公式$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-{y}_{i})^{2}}$,$\stackrel{∧}{a}$=y-$\stackrel{∧}{b}$x.
| 时间x | 1 | 1.5 | 2 | 2.5 | 3 |
| 命中率y | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
(Ⅱ)用线性回归分析方法,预测小李该月6号打3.5小时篮球的投篮命中率(保留2位小数点)
参考公式$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-{y}_{i})^{2}}$,$\stackrel{∧}{a}$=y-$\stackrel{∧}{b}$x.
11.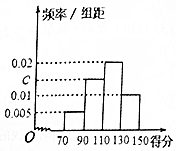 某校为了解校园安全管理专项活动的成效,对全校3000名学生进行一次安全意识测试,根据测试成绩评定“优秀”、“良好”、“及格”、“不及格”四个等级,现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.
某校为了解校园安全管理专项活动的成效,对全校3000名学生进行一次安全意识测试,根据测试成绩评定“优秀”、“良好”、“及格”、“不及格”四个等级,现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.
(Ⅰ)求a,b,c的值;
(Ⅱ)试估计该校安全意识测试评定为“优秀”的学生人数;
(Ⅲ)已知已采用分层抽样的方法,从评定等级为“优秀”和“良好”的学生中任选6人进行强化培训,现再从这6人中任选2人参加市级校园安全知识竞赛,求选取的2人中有1人为“优秀”的概率.
 某校为了解校园安全管理专项活动的成效,对全校3000名学生进行一次安全意识测试,根据测试成绩评定“优秀”、“良好”、“及格”、“不及格”四个等级,现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.
某校为了解校园安全管理专项活动的成效,对全校3000名学生进行一次安全意识测试,根据测试成绩评定“优秀”、“良好”、“及格”、“不及格”四个等级,现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.| 等级 | 不及格 | 及格 | 良好 | 优秀 |
| 得分 | [70,90) | [90,110) | [110,130) | [130,150] |
| 频数 | 6 | a | 24 | b |
(Ⅱ)试估计该校安全意识测试评定为“优秀”的学生人数;
(Ⅲ)已知已采用分层抽样的方法,从评定等级为“优秀”和“良好”的学生中任选6人进行强化培训,现再从这6人中任选2人参加市级校园安全知识竞赛,求选取的2人中有1人为“优秀”的概率.
18.已知集合M={x|(x-3)(x+1)≥0},N={x|-2≤x≤2},则M∩N=( )
| A. | [-2,-1] | B. | [-1,2] | C. | [-1,1] | D. | [1,2] |
8.已知双曲线:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1,F2,点P为双曲线右支上一点,若|PF1|2=8a|PF2|,则双曲线离心率的取值范围是( )
| A. | (1,3] | B. | [3,+∞) | C. | (0,3) | D. | (0,3] |
2.将函数$f(x)=\sqrt{3}sin\frac{x}{2}-cos\frac{x}{2}$的图象向右平移$\frac{2π}{3}$个单位长度得到函数y=g(x)的图象,则函数y=g(x)的一个单调减区间是( )
| A. | $(-\frac{π}{2},-\frac{π}{4})$ | B. | $(-\frac{π}{4},\frac{π}{2})$ | C. | $(\frac{π}{2},π)$ | D. | $(\frac{3π}{2},2π)$ |