题目内容
已知0<α<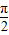 ,cosα=
,cosα= .
.(Ⅰ)求tanα的值;
(Ⅱ)求cos2α-cos(π-α)的值.
【答案】分析:(I)根据同角三角函数的平方关系,算出sinα=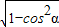 =
= ,再根据商数关系即可算出tanα的值;
,再根据商数关系即可算出tanα的值;
(II)利用二倍角的余弦公式和cos(π-α)的诱导公式化简,再代入(I)中的数据即可求出cos2α-cos(π-α)的值.
解答:解:(I)∵0<α<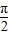 ,cosα=
,cosα= .
.
∴sinα=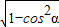 =
= ,
,
由此可得tanα=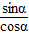 =
= ;
;
(II)∵cos2α=cos2α-sin2α=-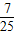 ,cos(π-α)=-cosα=-
,cos(π-α)=-cosα=-
∴cos2α-cos(π-α)=-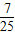 -(-
-(- )=
)=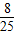 .
.
点评:本题给出锐角α满足的条件,求关于α的三角函数式的值.着重考查了同角三角函数的基本关系、诱导公式和二倍角三角公式等知识,属于基础题.
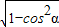 =
= ,再根据商数关系即可算出tanα的值;
,再根据商数关系即可算出tanα的值;(II)利用二倍角的余弦公式和cos(π-α)的诱导公式化简,再代入(I)中的数据即可求出cos2α-cos(π-α)的值.
解答:解:(I)∵0<α<
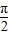 ,cosα=
,cosα= .
.∴sinα=
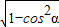 =
= ,
,由此可得tanα=
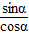 =
= ;
;(II)∵cos2α=cos2α-sin2α=-
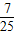 ,cos(π-α)=-cosα=-
,cos(π-α)=-cosα=-
∴cos2α-cos(π-α)=-
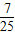 -(-
-(- )=
)=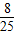 .
.点评:本题给出锐角α满足的条件,求关于α的三角函数式的值.着重考查了同角三角函数的基本关系、诱导公式和二倍角三角公式等知识,属于基础题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目