题目内容
已知0＜α＜π，sinα+cosα=
，求sinα和cosα的值．
| 1 | 5 |
分析：由条件求出 sinαcosα=-
＜0，由此可得sinα-cosα=
=
，解方程组求得sinα和cosα的值．
| 12 |
| 25 |
| (sinα-cosα)2 |
| 7 |
| 5 |
解答：解：由 sinα+cosα=
①，
两边平方，得sinαcosα=-
＜0．------（4分）
又0＜α＜π，∴sinα＞0，cosα＜0，则sinα-cosα＞0，
∴sinα-cosα=
=
=
②．----（8分）
由①②解得 sinα=
，cosα=-
．----（12分）
| 1 |
| 5 |
两边平方，得sinαcosα=-
| 12 |
| 25 |
又0＜α＜π，∴sinα＞0，cosα＜0，则sinα-cosα＞0，
∴sinα-cosα=
| (sinα-cosα)2 |
| 1-2sinαcosα |
| 7 |
| 5 |
由①②解得 sinα=
| 4 |
| 5 |
| 3 |
| 5 |
点评：本题主要考查同角三角函数的基本关系的应用，求出sinα-cosα=
，是解题的关键，属于基础题．
| 7 |
| 5 |
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
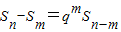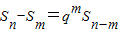恒成立．
恒成立．
恒成立．