题目内容
6.已知O,N,P在△ABC所在平面内,且|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|,$\overrightarrow{NA}$+$\overrightarrow{NB}$+$\overrightarrow{NC}$=$\overrightarrow{0}$,$\overrightarrow{PA}$•$\overrightarrow{PB}$=$\overrightarrow{PB}$•$\overrightarrow{PC}$=$\overrightarrow{PC}$•$\overrightarrow{PA}$,则点O,N,P依次是△ABC的( )| A. | 重心,外心,垂心 | B. | 重心,外心,内心 | C. | 外心,重心,垂心 | D. | 外心,重心,内心 |
分析 据O到三角形三个顶点的距离相等,得到O是三角形的外心,以NA,NB为邻边作平行四边形即可推出N在三角形的中线上,得出N为三角形的重心,将第三个条件两两相减,即可得到PA,PB,PC分别为三角形的高线,即P是三角形的垂心.
解答 解:(1)∵|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|,∴OA=OB=OC,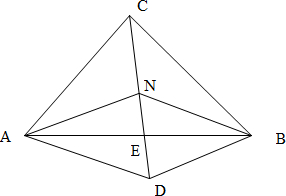
∴O是△ABC的外心.
(2)以NA,NB为邻边作平行四边形NADB,AB,ND交于点E,
则$\overrightarrow{NA}+\overrightarrow{NB}=\overrightarrow{ND}=2\overrightarrow{NE}$,E是AB的中点.
∵$\overrightarrow{NA}$+$\overrightarrow{NB}$+$\overrightarrow{NC}$=$\overrightarrow{0}$,∴$\overrightarrow{NA}+\overrightarrow{NB}=-\overrightarrow{NC}$,∴2$\overrightarrow{NE}$=$\overrightarrow{NC}$.
∴C,N,E三点共线,∴N在△ABC的边AB的中线上,
同理可得N在△ABC的另两边的中线上,
∴N为三角形ABC的重心.
(3)∵$\overrightarrow{PA}$•$\overrightarrow{PB}$=$\overrightarrow{PB}$•$\overrightarrow{PC}$,∴$\overrightarrow{PB}•$($\overrightarrow{PA}-\overrightarrow{PC}$)=0,即$\overrightarrow{PB}•\overrightarrow{AC}=0$,
∴PB⊥AC,
同理可证PA⊥BC,PC⊥AB,
∴P是△ABC的垂心.
故选:C.
点评 本小题主要考查向量的数量积的运算法则、三角形五心等基础知识,考查运算求解能力,考查化归与转化思想.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{\sqrt{13}}{2}$ | D. | $\frac{\sqrt{13}}{3}$ |
| A. | 14 | B. | ±10 | C. | -10 | D. | 10 |
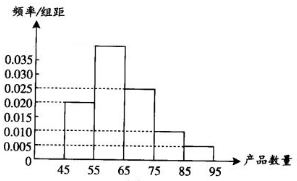 为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95)由此得到频率分布直方图如图.则产品数量位于[55,65)范围内的频率为0.4;这20名工人中一天生产该产品数量在[55,75)的人数是13.
为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95)由此得到频率分布直方图如图.则产品数量位于[55,65)范围内的频率为0.4;这20名工人中一天生产该产品数量在[55,75)的人数是13.