题目内容
设A={x|-3≤x≤3},B={y|y=-x2+t},若A∩B=∅,则实数t的取值范围是( )
| A、t<-3 | B、t≤-3 |
| C、t>3 | D、t≥3 |
考点:交集及其运算
专题:集合
分析:先求出B={y|y=-x2+t}={y|y≤t},再由A∩B=∅,结合不等式的性质能求出实数t的取值范围.
解答:
解:∵A={x|-3≤x≤3},
B={y|y=-x2+t}={y|y≤t},A∩B=∅,
∴t<-3.
故选:A.
B={y|y=-x2+t}={y|y≤t},A∩B=∅,
∴t<-3.
故选:A.
点评:本题考查实数t的取值范围的求法,是基础题,解题时要注意交集性质的合理运用.

练习册系列答案
相关题目
函数f(x)=ln(x+1)•tanx的图象可能是( )
A、 |
B、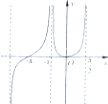 |
C、 |
D、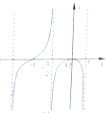 |
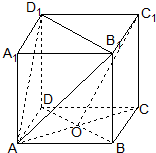 已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点.