题目内容
2.做一个圆柱形锅炉,容积为8π,两个底面的材料每单位面积的价格为2元,侧面的材料每单位面积的价格为4元.则当造价最低时,锅炉的底面半径与高的比为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
分析 设底面半径为r,根据体积得出底面半径与高的关系,得出造价关于底面半径的函数,使用基本不等式求出造价最小时的底面半径和高.
解答 解:设圆柱形锅炉的底面半径为r,高为h,则πr2h=8π,
∴h=$\frac{8}{{r}^{2}}$.
设锅炉的造价为y元,则y=2×2×πr2+4×2πr×h=4πr2+$\frac{64π}{r}$=4πr2+$\frac{32π}{r}$+$\frac{32π}{r}$≥3$\root{3}{{2}^{12}•{π}^{3}}$=48π.
当且仅当4πr2=$\frac{32π}{r}$即r=2时,取等号.此时h=$\frac{8}{{2}^{2}}=2$.
∴r:h=1.
故选B.
点评 本题考查了圆柱的面积,体积公式,基本不等式的应用,属于中档题.

练习册系列答案
相关题目
12.已知sin$\frac{θ}{2}$=$\frac{3}{5}$,cos$\frac{θ}{2}$=-$\frac{4}{5}$,则点P(cosθ,sinθ)位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
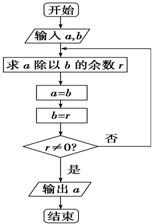 我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大的创举,这个伟大创举与古老的算法--“辗转相除法”实质一样,如图的程序框图源于“辗转相除法”.当输入a=6102,b=2016时,输出的a=18.
我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大的创举,这个伟大创举与古老的算法--“辗转相除法”实质一样,如图的程序框图源于“辗转相除法”.当输入a=6102,b=2016时,输出的a=18.