题目内容
20.已知函数f(x)=$\frac{x+a+|x-a|}{2}$,g(x)=ax+1,其中a>0.若f(x)与g(x)的图象有两个不同的交点,则a的取值范围是(0,1).分析 f(x)为分段函数,做出f(x)和g(x)图象,根据图象交点个数得出a的取值范围.
解答 解:f(x)=$\left\{\begin{array}{l}{x,x≥a}\\{a,x<a}\end{array}\right.$,
(1)若a<0,作出f(x)和g(x)的图象如图,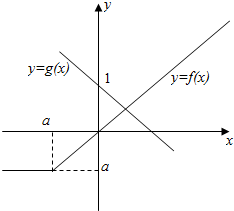
显然f(x)与g(x)只有一个交点.
(2)若a=0,作出f(x)和g(x)的图象如图,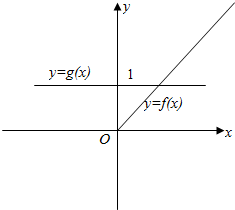
显然f(x)与g(x)只有一个交点.
(3)若a>1,作出f(x)和g(x)的图象如图,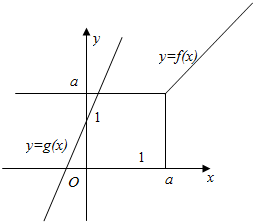
显然f(x)与g(x)只有一个交点.
(4)若0<a<1,作出f(x)和g(x)的图象如图,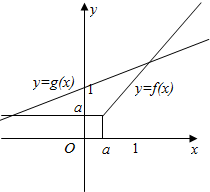
显然f(x)与g(x)有两个交点.
(5)若a=1,作出f(x)和g(x)的图象如图,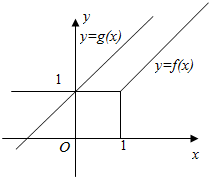
显然f(x)与g(x)只有一个交点.
综上,a的取值范围是(0,1).
故答案为(0,1).
点评 本题考查了函数图象的交点个数与分类讨论思想,正确作出函数图象是关键.

练习册系列答案
相关题目
10.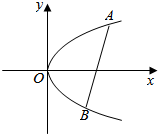 已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到y轴距离的最小值为 ( )
已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到y轴距离的最小值为 ( )
 已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到y轴距离的最小值为 ( )
已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到y轴距离的最小值为 ( )| A. | 2p | B. | $\frac{5}{2}p$ | C. | $\frac{3}{2}p$ | D. | 3p |
11.有编号为A1,A2,…,A9的9道题,其难度系数如表:
其中难度系数小于0.50的为难题.
(Ⅰ)从上述9道题中,随机抽取1道,求这道题为难题的概率;
(Ⅱ)从难题中随机抽取2道,求这两道题目难度系数相等的概率.
| 编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 |
| 难度系数 | 0.48 | 0.56 | 0.52 | 0.37 | 0.69 | 0.47 | 0.47 | 0.58 | 0.50 |
(Ⅰ)从上述9道题中,随机抽取1道,求这道题为难题的概率;
(Ⅱ)从难题中随机抽取2道,求这两道题目难度系数相等的概率.
15.设a,b,c∈R,下列命题正确的是( )
| A. | 若|a|<|b|,则|a+c|<|b+c| | B. | 若|a|<|b|,则|a-c|<|b-c| | C. | 若|a|<|b-c|,则|a|<|b|-|c| | D. | 若|a|<|b-c|,则|a|-|c|<|b| |
9.直线l1:2x-y-1=0与直线l2:mx+4y+2=0互相平行的充要条件是( )
| A. | m=-8 | B. | $m=-\frac{1}{2}$ | C. | m=8 | D. | m=2 |