题目内容
2.化简与求值:(不用计算器)(1)cos18°cos42°-sin18°sin42°;(2)cos80°sin70°+cos10°sin20°
(3)cos20°cos(α-20°)-cos70°sin(α-20°)(4)cos215°-cos275°.
分析 (1)利用两角和的余弦公式化简,再由特殊角的余弦值求值;
(2)利用诱导公式、两角和的正弦公式化简,再由特殊角的余弦值求值;
(3)利用两角和的余弦公式化简即可;
(4)利用诱导公式、二倍角的余弦公式化简,再由特殊角的余弦值求值.
解答 解:(1)cos18°cos42°-sin18°sin42°
=cos(18°+42°)=cos60°=$\frac{1}{2}$;
(in2)cos80°sin70°+cos10°sin20°
=cos(90°-10°)sin(90°-20°)+cos10°sin20°
=sin10°cos20°+cos10°sin20°=sin30°=$\frac{1}{2}$;
(3)cos20°cos(α-20°)-cos70°sin(α-20°)
=cos20°cos(α-20°)-sin20°sin(α-20°)
=cos[20°+(α-20°)]=cosα;
(4)cos215°-cos275°=cos215°-sin2(90°-15°)
=cos215°-sin215°=cos30°=$\frac{\sqrt{3}}{2}$.
点评 本题考查了两角和的正弦、余弦公式,二倍角的余弦公式,诱导公式,以及特殊角的余弦值,熟练掌握公式是解题的关键,考查化简、变形能力.

练习册系列答案
相关题目
12.函数f(x)=2sin(2x+$\frac{π}{6}$)的图象( )
| A. | 关于直线x=$\frac{π}{6}$对称 | B. | 关于直线x=-$\frac{π}{12}$对称 | ||
| C. | 关于点($\frac{2π}{3}$,0)对称 | D. | 关于点(π,0)对称 |
10.若实数x,y满足$\left\{{\begin{array}{l}{x≤2}\\{y≤3}\\{x+y≥1}\end{array}}\right.$,则z=3x+y的最大值为( )
| A. | 10 | B. | 9 | C. | 5 | D. | 2 |
17.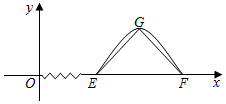 已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是以G为顶点,EF为底边且长为4的等腰直角三角形,则f(100)=( )
已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是以G为顶点,EF为底边且长为4的等腰直角三角形,则f(100)=( )
 已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是以G为顶点,EF为底边且长为4的等腰直角三角形,则f(100)=( )
已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是以G为顶点,EF为底边且长为4的等腰直角三角形,则f(100)=( )| A. | 0 | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |