题目内容
1. 如图,在直三棱柱ABC-A1B1C1中,底面△ABC是等腰直角三角形,且斜边$AB=\sqrt{2}$,侧棱AA1=2,点D为AB的中点,点E在线段AA1上,AE=λAA1(λ为实数).
如图,在直三棱柱ABC-A1B1C1中,底面△ABC是等腰直角三角形,且斜边$AB=\sqrt{2}$,侧棱AA1=2,点D为AB的中点,点E在线段AA1上,AE=λAA1(λ为实数).(1)求证:不论λ取何值时,恒有CD⊥B1E;
(2)当$λ=\frac{1}{3}$时,记四面体C1-BEC的体积为V1,四面体D-BEC的体积为V2,求V1:V2.
分析 (1)证明CD⊥AB,AA1⊥CD,然后证明CD⊥平面ABB1A1,推出CD⊥B1E.
(2)利用等体积法,转化求解即可.
解答 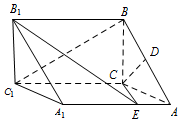 (1)证明:∵△ABC是等腰直角三角形,点D为AB的中点,
(1)证明:∵△ABC是等腰直角三角形,点D为AB的中点,
∴CD⊥AB.…(2分)
∵AA1⊥平面ABC,CD?平面ABC,∴AA1⊥CD.…(4分)
又∵AA1?平面ABB1A1,AB?平面ABB1A1,AA1∩AB=A,∴CD⊥平面ABB1A1.…(5分)
又∵B1E?平面ABB1A1,∴CD⊥B1E.…(6分)
(2)∵△ABC是等腰直角三角形,且斜边$AB=\sqrt{2}$,∴AC=BC=1.${V_1}={V_{{C_1}-CBE}}={V_{E-{C_1}BC}}=\frac{1}{3}AC•{S_{△{C_1}BC}}=\frac{1}{3}×\frac{1}{2}×1×1×2=\frac{1}{3}$,…(8分)${V_2}={V_{D-BEC}}={V_{E-CDB}}=\frac{1}{3}AE•{S_{△DBC}}=\frac{1}{3}×\frac{1}{2}×\frac{1}{2}×1×1×\frac{2}{3}=\frac{1}{18}$,…(11分)
所以V1:V2=6…(12分)
点评 本题考查直线与平面垂直的判定定理以及的应用,几何体的体积的求法,考查空间想象能力以及计算能力.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
9.函数y=x2-2x-3在区间[-1,4]的最值为( )
| A. | 最小值为-5,最大值为-4 | B. | 最小值为0,最大值为4 | ||
| C. | 最小值为-4,最大值为5 | D. | 最小值为0,最大值为5 |
16.若实数a、b、c>0,且${a^2}+ab+bc+ca=6-2\sqrt{5}$,则2a+b+c的最小值为( )
| A. | $\sqrt{5}-1$ | B. | $\sqrt{5}+1$ | C. | $2\sqrt{5}+2$ | D. | $2\sqrt{5}-2$ |
13.已知$x∈(-\frac{π}{2},0),tanx=-2$,则sin(x+π)=( )
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $-\frac{{\sqrt{5}}}{5}$ | C. | $-\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
10. 如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱A1A⊥面ABC,正视图是边长为2的正方形,该三棱柱的左视图面积为( )
如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱A1A⊥面ABC,正视图是边长为2的正方形,该三棱柱的左视图面积为( )
 如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱A1A⊥面ABC,正视图是边长为2的正方形,该三棱柱的左视图面积为( )
如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱A1A⊥面ABC,正视图是边长为2的正方形,该三棱柱的左视图面积为( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{3}$ |