Question

【题目】已知数列满足，且.

（1）求数列的通项公式；

（2）若数列的前项和为，且，，数列的前项和为，求满足的所有正整数的值.

Answer 1

【答案】（1）（2）所有正整数的值为2，3，4，5

【解析】

（1）先根据题中的递推关系式求得的值，得到，再利用求解，也可利用累乘法进行求解；

（2）先根据数列的通项与前项和之间的关系求得数列的通项公式，即可得到，再利用错位相减法求，最后根据的增减性求解即可.

（1）解法一由①，

得当时，，又，所以，

当时，②，

①-②，得，，即.

所以，

所以.

又也符合上式，所以.

解法二由①，

得当时，，又，所以，

当时，②，

①-②，得，即.

又也符合上式，所以，所以，

所以，

故数列的通项公式为.

（2）由③，

得当时，④，

③-④得，所以，

所以数列是以3为首项，3为公比的等比数列，

所以，

所以，

所以，

所以，

两式相减得，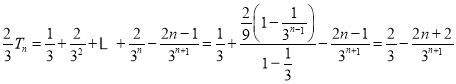

所以.

所以，

所以数列递增.

又，，，，

所以满足的所有正整数的值为2，3，4，5.