题目内容
已知抛物线y=x2-（k2+4）x-2k2-12，当抛物线与x轴的两交点间的距离最小时，求出此时k的值并求出最小的距离．
考点：二次函数的性质
专题：函数的性质及应用
分析：设抛物线与x轴的两交点间的横坐标分别为：x1，x2，由韦达定理得：x1+x2=k2+4，x1•x2=-2（k2+6），代入两交点间的距离d=|x1-x2|，求出即可．
解答：
解：设抛物线与x轴的两交点间的横坐标分别为：x1，x2，
由韦达定理得：x1+x2=k2+4，x1•x2=-2（k2+6），
则两交点间的距离d=|x1-x2|=
=k2+8，
∴k=0时，dmin=8．
由韦达定理得：x1+x2=k2+4，x1•x2=-2（k2+6），
则两交点间的距离d=|x1-x2|=
| (x1+x2)2-4x1x2 |
∴k=0时，dmin=8．
点评：本题考查了二次函数的性质，韦达定理，配方法，是一道基础题．
练习册系列答案
相关题目
如图，在直四棱ABCD-A1B1C1D1中（侧棱与底面垂直的棱柱叫直棱柱），底面ABCD是边长为4的菱形，且∠DAB=60°，AA1=2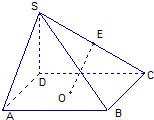
已知四棱锥S-ABCD中，底面ABCD为正方形，SD⊥DA，E为SC的中点，O为正方形ABCD的中心，AB=SD=6．