题目内容
17.已知△ABC中,M为线段BC上一点,AM=BM,$\overrightarrow{AM}$•$\overrightarrow{AB}$=2,AC2+3BC2=4,则△ABC的面积最大值为$\frac{1}{2}$.分析 由已知数量积求得c,由AC2+3BC2=4结合余弦定理可得$cosA=\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}=\frac{2{b}^{2}+4}{6b}=\frac{{b}^{2}+2}{3b}$,把三角形ABC的面积S=$\frac{1}{2}bc•sinA$转化为含有b的代数式,然后利用配方法求得最大值.
解答 解:如图,M为线段BC上一点,且AM=BM,
由$\overrightarrow{AM}$•$\overrightarrow{AB}$=2,得$\overrightarrow{AM}$•$\overrightarrow{AB}$=$|\overrightarrow{AM}||\overrightarrow{AB}|cos∠MAB=\frac{1}{2}|\overrightarrow{AB}{|}^{2}=2$,
∴$|\overrightarrow{AB}|=c=2$,
∵AC2+3BC2=4,即b2+3a2=4,
∴${a}^{2}=\frac{4-{b}^{2}}{3}$,
$cosA=\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}=\frac{2{b}^{2}+4}{6b}=\frac{{b}^{2}+2}{3b}$,
∴${S}_{△ABC}=\frac{1}{2}bc•sinA=b•\sqrt{1-co{s}^{2}A}$=$b•\sqrt{1-\frac{{b}^{4}+4{b}^{2}+4}{9{b}^{2}}}$
=b•$\sqrt{\frac{-{b}^{4}+5{b}^{2}-4}{9{b}^{2}}}=\frac{\sqrt{-{b}^{4}+5{b}^{2}-4}}{3}$=$\frac{\sqrt{-({b}^{2}-\frac{5}{2})^{2}+\frac{9}{4}}}{3}≤\frac{1}{2}$.
当且仅当${b}^{2}=\frac{5}{2}$时上式等号成立.
故答案为:$\frac{1}{2}$.
点评 本题考查平面向量的数量积运算,考查了正弦定理和余弦定理在求解三角形中的应用,是中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 4 | B. | 3$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
| A. | $\frac{12}{5}$ | B. | $\frac{13}{5}$ | C. | $\frac{5}{12}$ | D. | $\frac{5}{13}$ |

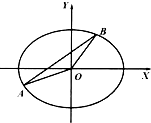 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,不经过原点O的直线l:y=kx+m(k>0)与椭圆E相交于不同的两点A、B,直线OA,AB,OB的斜率依次构成等比数列.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,不经过原点O的直线l:y=kx+m(k>0)与椭圆E相交于不同的两点A、B,直线OA,AB,OB的斜率依次构成等比数列.