题目内容
13. 如图,正方形ABCD的边长为6,点E,F分别在边AD,BC上,且DE=2AE,CF=2BF.如果对于常数λ,在正方形ABCD的四条边上,有且只有6个不同的点P使得$\overrightarrow{PE}•\overrightarrow{PF}=λ$成立,那么λ的取值范围是( )
如图,正方形ABCD的边长为6,点E,F分别在边AD,BC上,且DE=2AE,CF=2BF.如果对于常数λ,在正方形ABCD的四条边上,有且只有6个不同的点P使得$\overrightarrow{PE}•\overrightarrow{PF}=λ$成立,那么λ的取值范围是( )| A. | (0,7) | B. | (4,7) | C. | (0,4) | D. | (-5,16) |
分析 建立坐标系,逐段分析$\overrightarrow{PE}•\overrightarrow{PF}$的取值范围及对应的解,
解答 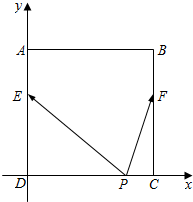 解:以DC为x轴,以DA为y轴建立平面直角坐标系,如图,则E(0,4),F(6,4).
解:以DC为x轴,以DA为y轴建立平面直角坐标系,如图,则E(0,4),F(6,4).
(1)若P在CD上,设P(x,0),0≤x≤6.∴$\overrightarrow{PE}$=(-x,4),$\overrightarrow{PF}$=(6-x,4).
∴$\overrightarrow{PE}•\overrightarrow{PF}$=x2-6x+16,∵x∈[0,6],∴7≤$\overrightarrow{PE}•\overrightarrow{PF}$≤16.
∴当λ=7时有一解,当7<λ≤16时有两解.
(2)若P在AD上,设P(0,y),0<y≤6.∴$\overrightarrow{PE}$=(0,4-y),$\overrightarrow{PF}$=(6,4-y).
∴$\overrightarrow{PE}•\overrightarrow{PF}$=(4-y)2=y2-8y+16,∵0<y≤6,∴0≤$\overrightarrow{PE}•\overrightarrow{PF}$<16.
∴当λ=0或4<λ<16,有一解,当0<λ≤4时有两解.
(3)若P在AB上,设P(x,6),0<x≤6.$\overrightarrow{PE}$=(-x,-2),$\overrightarrow{PF}$=(6-x,-2).
∴$\overrightarrow{PE}•\overrightarrow{PF}$=x2-6x+4,∵0<x≤6.∴-5≤$\overrightarrow{PE}•\overrightarrow{PF}$≤4.
∴当λ=-5或λ=4时有一解,当-5<λ<4时有两解.
(4)若P在BC上,设P(6,y),0<y<6,∴$\overrightarrow{PE}$=(-6,4-y),$\overrightarrow{PF}$=(0,4-y).
∴$\overrightarrow{PE}•\overrightarrow{PF}$=(4-y)2=y2-8y+16,∵0<y<6,∴0≤$\overrightarrow{PE}•\overrightarrow{PF}$<16.
∴当λ=0或4≤λ<16时有一解,当0<λ<4时有两解.
综上,∴0<λ<4.
故选:C.
点评 本题考查了平面向量的数量积计算,二次函数的根的个数判断.属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | (-∞,-1] | B. | (-∞,1] | C. | [-1,+∞) | D. | [1,+∞) |
| A. | $\overrightarrow{AB}-\overrightarrow{AC}$ | B. | $\overrightarrow{AB}+\overrightarrow{AC}$ | C. | $\frac{1}{2}(\overrightarrow{AB}-\overrightarrow{AC})$ | D. | $\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$ |

 某食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系$t=\left\{\begin{array}{l}64,x≤0\\{2^{kx+6}},x>0.\end{array}\right.$且该食品在4℃的保鲜时间是16小时.
某食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系$t=\left\{\begin{array}{l}64,x≤0\\{2^{kx+6}},x>0.\end{array}\right.$且该食品在4℃的保鲜时间是16小时.