题目内容
7.过抛物线y2=2px(p>0)的焦点F的直线l,依次分别交抛物线的准线、y轴、抛物线于A、B、C三点.若$\overrightarrow{{A}{B}}=2\overrightarrow{{B}C}$,则直线l的斜率是( )| A. | $-\sqrt{2}$或$\sqrt{2}$ | B. | -2或2 | C. | $-2\sqrt{2}$或$2\sqrt{2}$ | D. | -4或4 |
分析 如图所示,设直线l的方程为:$y=k(x-\frac{p}{2})$,与抛物线方程联立可得${y}^{2}-\frac{2p}{k}y-{p}^{2}$=0,解得yC,由直线l的方程为:$y=k(x-\frac{p}{2})$,可得yA=-pk,yB=-$\frac{pk}{2}$.由于$\overrightarrow{{A}{B}}=2\overrightarrow{{B}C}$,可得yB-yA=2(yC-yB),代入解出即可.
解答 解:如图所示,
设直线l的方程为:$y=k(x-\frac{p}{2})$,
联立$\left\{\begin{array}{l}{y=k(x-\frac{p}{2})}\\{{y}^{2}=2px}\end{array}\right.$,化为${y}^{2}-\frac{2p}{k}y-{p}^{2}$=0,
解得yC=$\frac{p(1-\sqrt{1+{k}^{2}})}{k}$,
由直线l的方程为:$y=k(x-\frac{p}{2})$,
可得yA=-pk,yB=-$\frac{pk}{2}$.
∵$\overrightarrow{{A}{B}}=2\overrightarrow{{B}C}$,
∴yB-yA=2(yC-yB),
即3yB-yA=2yC,
∴$-\frac{3pk}{2}+pk=\frac{2p(1-\sqrt{1+{k}^{2}})}{k}$,
化为k4-8k2=0,k≠0,
化为k2-8=0,
解得k=$±2\sqrt{2}$.
故选:C.
点评 本题考查了抛物线的标准方程及其性质、直线与抛物线相交问题、向量的线性运算,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12. 如图,一条直线与抛物线y2=2px(p>0)交于A、B两点,且OA⊥OB,OD⊥AB于D,若点D的坐标为(2,1),则抛物线方程为( )
如图,一条直线与抛物线y2=2px(p>0)交于A、B两点,且OA⊥OB,OD⊥AB于D,若点D的坐标为(2,1),则抛物线方程为( )
 如图,一条直线与抛物线y2=2px(p>0)交于A、B两点,且OA⊥OB,OD⊥AB于D,若点D的坐标为(2,1),则抛物线方程为( )
如图,一条直线与抛物线y2=2px(p>0)交于A、B两点,且OA⊥OB,OD⊥AB于D,若点D的坐标为(2,1),则抛物线方程为( )| A. | y2=$\frac{5}{4}$x | B. | y2=$\frac{5}{2}$x | C. | y2=5x | D. | y2=10x |
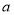 ,
,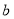 ,
, 是正数,求证:
是正数,求证: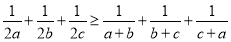 .
.  ,
, ,则
,则 等于( )
等于( ) B.
B.
 D.
D.
 满足
满足 ,则
,则 与
与 的夹角是( )
的夹角是( ) B.
B.
 D.
D.