题目内容
19.已知函数f(x)=Asin(ωx+$\frac{π}{6}$)(A>0,ω>0)的图象在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+$\frac{π}{2}$,-2).(1)求函数f(x)的解析式;
(2)求sin(x0+$\frac{π}{4}$)的值.
分析 (1)根据条件求出振幅以及函数的周期,即可求函数f(x)的解析式;
(2)根据函数的最值,求出x0的大小,结合两角和差的正弦公式进行求解即可.
解答 解:(1)∵图象在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+$\frac{π}{2}$,-2).
∴A=2,$\frac{T}{2}$=x0+$\frac{π}{2}$-x0=$\frac{π}{2}$,
即函数的周期T=π,即T=$\frac{2π}{ω}=π$,解得ω=2,
即f(x)=2sin(2x+$\frac{π}{6}$).
(2)∵函数的最高点的坐标为(x0,2),
∴2x0+$\frac{π}{6}$=$\frac{π}{2}$,
即x0=$\frac{π}{6}$,
则sin(x0+$\frac{π}{4}$)=sin($\frac{π}{6}$+$\frac{π}{4}$)=sin$\frac{π}{6}$cos$\frac{π}{4}$+cos$\frac{π}{6}$sin$\frac{π}{4}$
=$\frac{\sqrt{2}}{2}$(sin$\frac{π}{6}$+cos$\frac{π}{6}$)=$\frac{\sqrt{2}}{2}$($\frac{1}{2}+\frac{\sqrt{3}}{2}$)=$\frac{\sqrt{2}+\sqrt{6}}{4}$.
点评 本题主要考查三角函数的解析式的求解,以及三角函数值的计算,利用两角和差的正弦公式是解决本题的关键.

练习册系列答案
相关题目
7.过抛物线y2=2px(p>0)的焦点F的直线l,依次分别交抛物线的准线、y轴、抛物线于A、B、C三点.若$\overrightarrow{{A}{B}}=2\overrightarrow{{B}C}$,则直线l的斜率是( )
| A. | $-\sqrt{2}$或$\sqrt{2}$ | B. | -2或2 | C. | $-2\sqrt{2}$或$2\sqrt{2}$ | D. | -4或4 |
14.点P在抛物线y2=8x上,点Q在圆(x-6)2+y2=1上,则|PQ|的最小值为( )
| A. | 5 | B. | 6 | C. | 4$\sqrt{2}$ | D. | 4$\sqrt{2}$-1 |
11.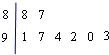 若某市8所中学参加中学生合唱比赛的得分用茎叶图表示(如图1),其中茎为十位数,
若某市8所中学参加中学生合唱比赛的得分用茎叶图表示(如图1),其中茎为十位数,
叶为个位数,则这组数据的中位数和平均数分别是( )
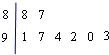 若某市8所中学参加中学生合唱比赛的得分用茎叶图表示(如图1),其中茎为十位数,
若某市8所中学参加中学生合唱比赛的得分用茎叶图表示(如图1),其中茎为十位数,叶为个位数,则这组数据的中位数和平均数分别是( )
| A. | 91,91.5 | B. | 91,92 | C. | 91.5,91.5 | D. | 91.5,92 |
8.设非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{c}$|,|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{c}$|,则向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
 ,若
,若 ,则
,则 、
、 、
、 的大小关系为( )
的大小关系为( ) B.
B.
 D.
D.
 是三个全等的菱形,
是三个全等的菱形, ,设
,设 .已知点
.已知点 在各菱形边上运动,且
在各菱形边上运动,且 的最大值为( )
的最大值为( )