Question

数列{a_n}中，S_n是其前n项和，若a₁=1，a_n+1=S_n（n≥1），则a_n=________．

Answer 1

分析：由，得（n≥2），作差可得a_n，a_n+1间的递推关系式，由递推式及首项可判断该数列从第二项起构成等比数列，从而可求得通项公式．
解答：由，得（n≥2），
两式相减得a_n+1-a_n=，即（n≥2），
又a₁=1，，
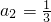所以数列{a_n}中各项均不为0，且从第二项起构成公比为的等比数列，
所以n≥2时，，n=1时，a₁=1，
所以a_n=，
故答案为：．
点评：本题考查由数列递推公式求数列通项公式，解决本题的基础是正确理解a_n与S_n间的关系．