题目内容
(本小题满分12分,(1)小问3分,(2)小问4分,(3)小问5分)
对于函数 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式 对定义域中的每一个
对定义域中的每一个 都成立,则称函数
都成立,则称函数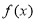 是“(
是“( )型函数”.
)型函数”.
(1)判断函数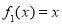 是否为 “(
是否为 “( )型函数”,并说明理由;
)型函数”,并说明理由;
(2)若函数 是“(
是“( )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对 ;
;
(3)已知函数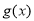 是“(
是“( )型函数”,对应的实数对
)型函数”,对应的实数对 为(1,4).当
为(1,4).当 时,
时,

 ,若当
,若当 时,都有
时,都有 ,试求
,试求 的取值范围.
的取值范围.
(1)不是,理由见解析;(2)a=1,b=16;(3)
【解析】
试题分析:(1) 不是“(
不是“( )型函数”,因为不存在实数对
)型函数”,因为不存在实数对 使得
使得 ,
,
即 对定义域中的每一个x都成立;
对定义域中的每一个x都成立;
(2)由 ,可得
,可得 ,所以存在实数对,如a=1,b=16,使得
,所以存在实数对,如a=1,b=16,使得 对任意的
对任意的
X∈R都成立
(3)由题意得, ,所以当
,所以当 时,
时,  ,其中
,其中 ,而
,而 时,
时, ,且其对称轴方程为
,且其对称轴方程为 .
.
当 ,即
,即 时,
时, 在
在 上的值域为
上的值域为 ,即
,即 ,则
,则 在
在 上的值域为
上的值域为 ,由题意得
,由题意得 ,从而
,从而 ;
;
当 ,即
,即 时,
时, 的值域为
的值域为 ,即
,即 ,则
,则 在
在 上的值
上的值
域为 ,则由题意得
,则由题意得 且
且 ,解得
,解得
当 ,即
,即 时,g(x)的值域为
时,g(x)的值域为 ,即
,即 ,则g(x)在[0,2]上的值域为
,则g(x)在[0,2]上的值域为
 ,
,
则 ,解得
,解得 .
.
综上所述,所求m的取值范围是 .
.
考点:新定义问题;函数恒成立问题的处理方法

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
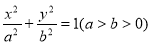 的离心率为
的离心率为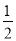 ,其左焦点
,其左焦点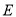 与抛物线
与抛物线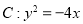 的焦点相同.
的焦点相同.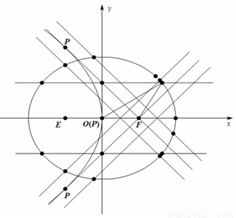
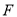 的直线
的直线 与曲线
与曲线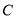 只有一个交点
只有一个交点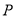 ,则
,则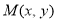 ,使得
,使得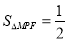 ,若存在,请说明一共有几个点;若不存在,请说明理由.
,若存在,请说明一共有几个点;若不存在,请说明理由.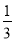 ,某植物研究所进行该种子的发芽实验,每次实验种一粒种子,每次实验结果相互独立,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败.若该研究所共进行四次实验,设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值.
,某植物研究所进行该种子的发芽实验,每次实验种一粒种子,每次实验结果相互独立,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败.若该研究所共进行四次实验,设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值.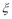 x-1在区间(2,3)上有且只有一个零点”为事件A,求事件A发生的概率P(A).
x-1在区间(2,3)上有且只有一个零点”为事件A,求事件A发生的概率P(A). 对任意
对任意 恒成立,则实数x的取值范围是( )
恒成立,则实数x的取值范围是( )  B.
B.
 D.
D.
 满足约束条件
满足约束条件 ,则
,则 的最小值为( )
的最小值为( ) B.
B. C.
C.  D.
D. 


 是定义域为R的奇函数,且当
是定义域为R的奇函数,且当 时,
时, .则函数
.则函数 的零点的个数为( )
的零点的个数为( )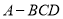 中,
中,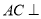 底面
底面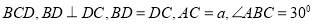 ,则点
,则点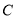 到平面
到平面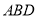 的距离是_____________。
的距离是_____________。 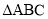 中,
中,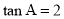 ,
, .
.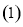 求角
求角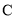 的值;
的值; 设
设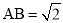 ,求
,求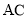 .
.