研究某校女学生身高和体重的关系.用相关指数R2来刻画回归效果时.如果可以叙述为“身高解释了64%的体重变化.而随机误差贡献了剩余的36%.所以身高对体重的效应比随机误差的效应大得多 .则相关指数R2≈0.64．题目和参考答案——青夏教育精英家教网——

题目内容

17．研究某校女学生身高和体重的关系，用相关指数R²来刻画回归效果时，如果可以叙述为“身高解释了64%的体重变化，而随机误差贡献了剩余的36%，所以身高对体重的效应比随机误差的效应大得多”，则相关指数R²≈0.64．

分析用相关系数r衡量两个变量之间的相关关系的强弱时，根据“身高解释了64%的体重变化”得出相关指数的大小．

解答解：用相关系数r可以衡量两个变量之间的相关关系的强弱，
因为身高解释了64%的体重变化，而随机误差贡献了剩余的36%，
所以得出相关指数R²≈0.64．
故答案为：0.64．

点评本题考查了相关系数、两个变量线性相关的强弱的判断问题，是基础题．

练习册系列答案

黄冈经典阅读系列答案

文言文课外阅读特训系列答案

轻松阅读训练系列答案

南大教辅初中英语任务型阅读与首字母填空系列答案

初中英语听力与阅读系列答案

领航英语阅读理解与完形填空系列答案

英语拓展听力与阅读系列答案

阅读组合突破系列答案

初中英语阅读系列答案

全程探究阅读系列答案

相关题目

7．已知在△ABC所在平面内有两点P、Q，满足$\overrightarrow{PA}$+$\overrightarrow{PC}$=0，$\overrightarrow{QA}$+$\overrightarrow{QB}$+$\overrightarrow{QC}$=$\overrightarrow{BC}$，若|$\overrightarrow{AB}$|=4，|$\overrightarrow{AC}$|=2，S_△APQ=$\frac{2}{3}$，则$\overrightarrow{AB}$•$\overrightarrow{AC}$的值为±4$\sqrt{3}$．

8．若sin（π-α）=-$\frac{{\sqrt{3}}}{3}$，且α∈（π，$\frac{3π}{2}$），则sin（$\frac{π}{2}$+α）=（　　）

-$\frac{\sqrt{6}}{3}$

-$\frac{\sqrt{6}}{6}$

$\frac{\sqrt{6}}{6}$

$\frac{\sqrt{6}}{3}$

5．给出下列四个命题，其中正确的是（　　）
①空间四点共面，则其中必有三点共线；
②空间四点不共面，则其中任何三点不共线；
③空间四点中存在三点共线，则此四点共面；
④空间四点中任何三点不共线，则此四点不共面．

12．设f（x）为可导函数，且满足$\underset{lim}{x→0}$$\frac{f（1）-f（1+2x）}{2x}$=1，则曲线y=f（x）在点（1，f（1））处的切线的斜率为（　　）

2．若直线l：y=kx与曲线C：$\left\{\begin{array}{l}x=2+cosθ\\ y=sinθ\end{array}$（参数θ∈R）有唯一的公共点，则实数k等于（　　）

$\frac{\sqrt{3}}{3}$

-$\frac{\sqrt{3}}{3}$

±$\frac{\sqrt{3}}{3}$

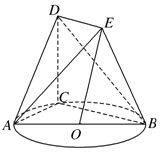如图，点C是以AB为直径的圆上一点，直角梯形BCDE所在平面与圆O所在平面垂直，且DE∥BC，DC⊥BC，DE=1，BC=2，AC=CD=3
（1）证明：EO∥平面ACD；
（2）证明：平面ACD⊥平面BCDE；
（3）求三棱锥E-ABD的体积．

6．一个扇形OAB的面积为1平方厘米，它的周长为4厘米，则它的中心角是（　　）

7．已知函数f（x）=$\left\{\begin{array}{l}{2-|x|，x≤2}\\{（x-2）^{2}，x＞2}\end{array}\right.$函数g（x）=f（2-x）-$\frac{1}{4}$b，其中b∈R，若函数y=f（x）+g（x）恰有4个零点，则b的取值范围是（　　）