题目内容
若（1-x）2011=a0+a1x+…+a2011x2011（x∈R），则a1+…+a2011=（ ）
| A、2 | B、0 | C、-1 | D、-2 |
考点：二项式系数的性质
专题：二项式定理
分析：在所给的等式中，令x=0可得a0=1，在所给的等式中，再令x=1可得a0+a1+…+a2011=0，从而求得a1+…+a2011的值．
解答：
解：在（1-x）2011=a0+a1x+…+a2011x2011（x∈R）中，令x=0，可得a0=1．
在（1-x）2011=a0+a1x+…+a2011x2011（x∈R）中，再令x=1可得a0+a1+…+a2011=0，
∴a1+…+a2011=-1，
故选：C．
在（1-x）2011=a0+a1x+…+a2011x2011（x∈R）中，再令x=1可得a0+a1+…+a2011=0，
∴a1+…+a2011=-1，
故选：C．
点评：本题主要考查二项式定理的应用，是给变量赋值的问题，关键是根据要求的结果，选择合适的数值代入，属于基题．
练习册系列答案
名校课堂系列答案
相关题目
双曲线M：
-
=1（a＞0，b＞0）实轴的两个顶点为A，B，点P为双曲线M上除A、B外的一个动点，若QA⊥PA且QB⊥PB，则动点Q的运动轨迹为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
不等式
≤-1的解集是（ ）
| 3x-1 |
| x-2 |
A、{x|
| ||
B、{x|
| ||
C、{x|x＞2或x≤
| ||
| D、{x|x＜2} |
由①正方形的对角线相等；②矩形的对角线相等；③正方形是矩形．写一个“三段论”形式的推理，则作为大前提、小前提和结论的分别为（ ）
| A、②①③ | B、③①② |
| C、①②③ | D、②③① |
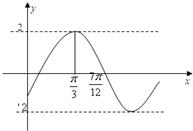已知函数y=Asin（ωx+φ）（ω＞0，A＞0，|φ|＜| π |
| 2 |
A、y=sin（2x+
| ||
B、y=2sin（x-
| ||
C、y=2sin（2x-
| ||
D、y=2sin（2x+
|
过点（2，
）且平行于极轴的直线的极坐标方程是（ ）
| π |
| 4 |
| A、ρcosθ=4 | ||
| B、ρsinθ=4 | ||
C、ρsinθ=
| ||
D、ρcosθ=
|
若|x|≤
，则函数f（x）=cos2x+sinx的最小值是（ ）
| π |
| 4 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
椭圆
+
=1（m＞0，n＞0）一个焦点坐标是（2，0），且椭圆的离心率e=
，则椭圆标准方程（ ）
| x2 |
| m2 |
| y2 |
| n2 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|