题目内容
如图，正三棱柱ABC-A1B1C1中，底面边长是2，侧棱长为4，M，N分别在AA1和CC1上，A1M=CN=1，P是BC中点．（1）求四面体A1-PMN的体积；
（2）证明A1B∥平面PMN．
考点：直线与平面平行的判定,棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：（1）由VA1-PMN=VP-A1MN，利用等积法能求出四面体A1-PMN的体积．
（2）取CC1的中点R，由已知条件推导出四边形A1RNM是平行四边形，由此能证明平面A1RB∥平面PMN，从而得到A1B∥平面PMN．
（2）取CC1的中点R，由已知条件推导出四边形A1RNM是平行四边形，由此能证明平面A1RB∥平面PMN，从而得到A1B∥平面PMN．
解答：
（1）解：取AC的中点O，由已知得BO⊥A1MN，且BO=
，
∵P是BC中点，∴P到平面A1MN的距离d=
BO=
，
又S△A1MN=
×1×2=1，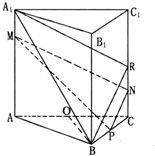
∴VA1-PMN=VP-A1MN=
S△A1MN×d=
×1×
=
．
（2）证明：取CC1的中点R，
∵P是BC的中点，N是RC的中点，∴PN∥BR，
又A1M∥RN，A1M=RN，
∴四边形A1RNM是平行四边形，
从而A1R∥MN，
又A1R∩BR=R，∴平面A1RB∥平面PMN，
又A1B?平面A1RB，∴A1B∥平面PMN．
| 3 |
∵P是BC中点，∴P到平面A1MN的距离d=
| 1 |
| 2 |
| ||
| 2 |
又S△A1MN=
| 1 |
| 2 |
∴VA1-PMN=VP-A1MN=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 6 |
（2）证明：取CC1的中点R，
∵P是BC的中点，N是RC的中点，∴PN∥BR，
又A1M∥RN，A1M=RN，
∴四边形A1RNM是平行四边形，
从而A1R∥MN，
又A1R∩BR=R，∴平面A1RB∥平面PMN，
又A1B?平面A1RB，∴A1B∥平面PMN．
点评：本题考查四面体体积的求法，考查直线与平面平行的证明，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
A={1，2}，集合B={2，3}，则 A∪B=（ ）
| A、{1，2，2，3} |
| B、{2} |
| C、{1，2，3} |
| D、{1，3} |
若函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，在五面体ABCDEF中，四边形ABCD是矩形，DE⊥平面ABCD．