题目内容
3.已知lg2y+(2x+1+2-x+1)lgy+(22x+1+2-2x+1)=0,求x、y的值.分析 化简△=(2x+1+2-x+1)2-4(22x+1+2-2x+1)=-(2x+1-2-x+1)2≤0,从而解得x=0,从而代入求解.
解答 解:∵△=(2x+1+2-x+1)2-4(22x+1+2-2x+1)
=22x+2+2-2x+2+2•2x+12-x+1-2(22x+2+2-2x+2)
=-(2x+1-2-x+1)2≤0,
依题意,△≥0,
故2x+1=2-x+1,
故x=0,
当x=0时,lg2y+4lgy+4=0,
故lgy=-2,
故y=$\frac{1}{100}$.
点评 本题考查了二次方程的解法与对数运算及指数运算的应用.

练习册系列答案
相关题目
13.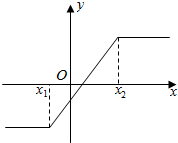 对任意的x1<0<x2,若函数f(x)=a|x-x1|+b|x-x2|的图象为如图所示的一条折线(两侧的射线均平行于x轴),则实数a、b应满足的条件是( )
对任意的x1<0<x2,若函数f(x)=a|x-x1|+b|x-x2|的图象为如图所示的一条折线(两侧的射线均平行于x轴),则实数a、b应满足的条件是( )
 对任意的x1<0<x2,若函数f(x)=a|x-x1|+b|x-x2|的图象为如图所示的一条折线(两侧的射线均平行于x轴),则实数a、b应满足的条件是( )
对任意的x1<0<x2,若函数f(x)=a|x-x1|+b|x-x2|的图象为如图所示的一条折线(两侧的射线均平行于x轴),则实数a、b应满足的条件是( )| A. | a+b=0且a-b>0 | B. | a+b=0且a-b<0 | C. | a-b=0且a+b>0 | D. | a-b=0且a+b<0. |
11.已知数列{an}是公比为q(q>0)的等比数列,其中a4=1,且a2,a3,a3-2成等差数列.
(1)求数列{an}的通项公式;
(2)记数列{an}的前n项和为Sn,求证:Sn<16(n∈N+)
(1)求数列{an}的通项公式;
(2)记数列{an}的前n项和为Sn,求证:Sn<16(n∈N+)
15.函数f(x)在定义域x∈R上,是以5为周期的奇函数,且f(-2)=1,则f(12)等于( )
| A. | 1 | B. | -1 | C. | 5 | D. | -5 |
12.已知i为虚数单位,复数z满足zi=$\frac{3-i}{1+i}$,则复数z的模|z|=( )
| A. | $\sqrt{3}$ | B. | 4 | C. | $\sqrt{5}$ | D. | 2 |
 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:AB=3:4,AE=6,则AC等于( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:AB=3:4,AE=6,则AC等于( )