题目内容
15.已知动圆C与直线x+y+2=0相切于点A(0,-2),圆C被x轴所截得的弦长为2,则满足条件的所有圆C的半径之和是6$\sqrt{2}$.分析 由题意,圆心在直线x-y-2=0上,设圆心为(a,a-2),则R=$\frac{|2a|}{\sqrt{2}}$=$\sqrt{2}$|a|=$\sqrt{1+(a-2)^{2}}$,求出a,可得半径,即可求出满足条件的所有圆C的半径之和.
解答 解:由题意,圆心在直线x-y-2=0上,设圆心为(a,a-2),则R=$\frac{|2a|}{\sqrt{2}}$=$\sqrt{2}$|a|=$\sqrt{1+(a-2)^{2}}$,
∴a=1或-5,
∴R=$\sqrt{2}$或5$\sqrt{2}$,
∴满足条件的所有圆C的半径之和是6$\sqrt{2}$.
故答案为:6$\sqrt{2}$.
点评 本题考查圆的方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
6.不等式组$\left\{\begin{array}{l}{(x-y+1)(x+y-1)≥0}\\{-2≤x≤0}\end{array}\right.$表示的平面区域的面积是( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
10.若图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则这个几何体外接球的表面积为( )
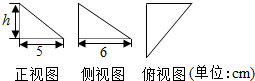

| A. | 25xcm2 | B. | $\frac{77π}{2}$cm2 | C. | 77πcm2 | D. | 144πcm2 |