题目内容
6.不等式组$\left\{\begin{array}{l}{(x-y+1)(x+y-1)≥0}\\{-2≤x≤0}\end{array}\right.$表示的平面区域的面积是( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 作出不等式组对应的平面区域,结合图形的面积公式进行求解即可.
解答 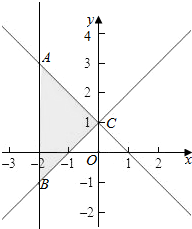 解:不等式组等价为$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-1≥0}\\{-2≤x≤0}\end{array}\right.$或$\left\{\begin{array}{l}{x-y+1≤0}\\{x+y-1≤0}\\{-2≤x≤0}\end{array}\right.$,
解:不等式组等价为$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-1≥0}\\{-2≤x≤0}\end{array}\right.$或$\left\{\begin{array}{l}{x-y+1≤0}\\{x+y-1≤0}\\{-2≤x≤0}\end{array}\right.$,
则对应的区域为:
则对应的区域为三角形ABC,C(0,1),
由$\left\{\begin{array}{l}{x=-2}\\{x-y+1=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$,即B(-2,-1),
由$\left\{\begin{array}{l}{x=-2}\\{x+y-1=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$,即A(-2,3),
则△ABC的面积S=$\frac{1}{2}×1×[3-(-1)]=\frac{1}{2}×4$=2,
故选:A.
点评 本题主要考查二元一次不等式组表示平面区域,以及三角形面积的计算,根据条件作出平面区域是解决本题的关键.

练习册系列答案
相关题目
1.为了考察高中生的性别与是否喜欢数学课程之间的关系,在我市的某校高中生中随即抽取了100名学生,得到如下联表:
由表中数据,计算得K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$≈3.03,
附表:
参照附表,则下列结论正确的是( )
| 不喜欢数学课程 | 喜欢数学课程 | 总计 | |
| 男 | 45 | 10 | 55 |
| 女 | 30 | 15 | 45 |
| 总 | 75 | 25 | 100 |
附表:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 |
| k0 | 2.706 | 3.841 | 5.024 |
| A. | 有90%以上的把握认为“性别与是否喜欢数学课程有关” | |
| B. | 有90%以上的把握认为“性别与是否喜欢数学课程没有关” | |
| C. | 在犯错误的概率不超过1%的前提下,认为“性别与是否喜欢数学课程有关” | |
| D. | 在犯错误的概率不超过1%的前提下,认为“性别与是否喜欢数学课程没有关” |
11.已知集合A={x|x≥1},B={x|-2≤x≤2},则A∩B等于( )
| A. | {x|1≤x≤2} | B. | {x|-2≤x≤1} | C. | {x|x≥-2} | D. | {x|x≤2} |