题目内容
已知⊙O:x2+y2=6,P为⊙O上动点,过P作PM⊥x轴于M,N为PM上一点,且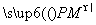 =
=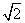
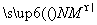 .
.
(1)求点N的轨迹C的方程;
(2)若A(2,1),B(3,0),过B的直线与曲线C相交于D,E两点,则kAD+kAE是否为定值?若是,求出该值;若不是,说明理由.
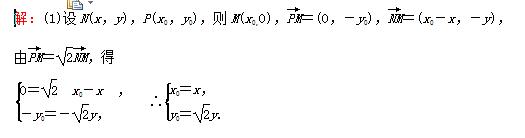 由于点P在⊙O:x2+y2=6上,则有x2+(
由于点P在⊙O:x2+y2=6上,则有x2+(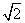 y)2=6,即
y)2=6,即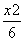 +
+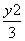 =1.∴点N的轨迹C的方程为
=1.∴点N的轨迹C的方程为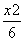 +
+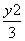 =1.
=1.
(2)设D(x1,y1),E(x2,y2),过点B的直线DE的方程为y=k(x-3),
由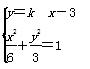 消去y,得(2k2+1)x2-12k2x+18k2-6=0,其中Δ>0,
消去y,得(2k2+1)x2-12k2x+18k2-6=0,其中Δ>0,
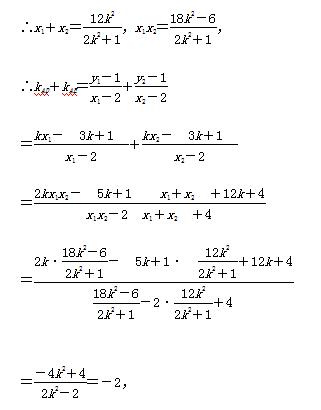 ∴kAD+kAE是定值-2.
∴kAD+kAE是定值-2.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
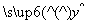 =1.23x+0.08;
=1.23x+0.08;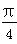 ;
;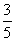 a,则
a,则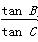 =________.
=________.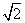 -4 B.
-4 B.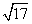 -1 C.6-2
-1 C.6-2 图象上任意一点,点Q(2a,a-3)(a∈R),则|PQ|的最小值为( )
图象上任意一点,点Q(2a,a-3)(a∈R),则|PQ|的最小值为( )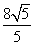 -2 B.
-2 B.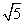 C.
C.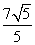 -2
-2
 的渐近线方程为
的渐近线方程为 ,则以它的顶点为焦点,焦点为顶点的椭圆的离心率等于
,则以它的顶点为焦点,焦点为顶点的椭圆的离心率等于 C.
C. D.
D.