题目内容
若复数z满足|z+3+4i|=6，则|z|的最小值和最大值分别为（ ）
| A、1和11 | B、0和11 |
| C、5和6 | D、0和1 |
考点：复数求模
专题：数系的扩充和复数
分析：可得复数z对应的点在以A（-3，-4）为圆心以6为半径的圆周，结合图象可得|z|的最小值和最大值．
解答：
解：由|z+3+4i|=6得|z-（-3-4i）|=6，
∴复数z对应的点在以A（-3，-4）为圆心以6为半径的圆周，
可得|OA|=
=5，
∴|z|的最小值为：6-5=1，
∴|z|的最大值为：6+5=11．
故选：A．
解：由|z+3+4i|=6得|z-（-3-4i）|=6，∴复数z对应的点在以A（-3，-4）为圆心以6为半径的圆周，
可得|OA|=
| (-3)2+(-4)2 |
∴|z|的最小值为：6-5=1，
∴|z|的最大值为：6+5=11．
故选：A．
点评：本题考查复数的代数形式和几何意义，属中档题．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
函数f（x）的定义域为R，其导函数f′（x）的图象如图所示，则函数f（x）（ ）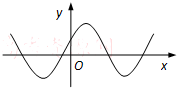
| A、有三个极值点，但无法判断有几个极大值，几个极小值 |
| B、有一个极大值点，两个极小值点 |
| C、有两个极大值点，两个极小值点 |
| D、有四个极值点，但无法判断有几个极大值，几个极小值 |
函数f（x）=cos（x2+x）导数是（ ）
| A、-sin（x2+x） |
| B、-（2x+1）sin（x2+x） |
| C、-2xsin（x2+x） |
| D、（2x+1）sin（x2+x） |
已知A（-1，-2，6），B（1，2，-6）O为坐标原点，则向量
与
的夹角是（ ）
| OA |
| OB |
| A、0 | ||
B、
| ||
| C、π | ||
D、
|
已知点（-1，-1）在直线ax+by+2=0（a＞0，b＞0）上，则
+
的最小值为（ ）
| 1 |
| a |
| 1 |
| b |
| A、1 | B、2 | C、3 | D、4 |
若函数y=x2-3x-4的定义域为[0，m]，值域为[-
，-4]，则m的取值范围是（ ）
| 25 |
| 4 |
| A、（0，4] | ||
B、[
| ||
C、[
| ||
D、[
|
某射击运动员射击所得环数ξ的分布列如下所示，则P（ξ=8）=（ ）
| ξ | 7 | 8 | 9 | 10 |
| P | 0.21 | m | 0.29 | 0.22 |
| A、0.31 | B、0.38 |
| C、0.41 | D、0.28 |
设i为虚数单位，则
=（ ）
| 2 |
| i-1 |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
如果命题p（n）对n=k成立（n∈N*），则它对n=k+2也成立，若p（n）对n=2成立，则下列结论正确的是（ ）
| A、p（n）对一切正整数n都成立 |
| B、p（n）对任何正偶数n都成立 |
| C、p（n）对任何正奇数n都成立 |
| D、p（n）对所有大于1的正整数n都成立 |