题目内容
若关于x的不等式ax2+bx+a2-1≤0的解集为[-1，+∞），则实数a，b的值分别为多少？
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：根据题意，得出a=0，是一元一次不等式，从而求出b的值．
解答：
解：∵关于x的不等式ax2+bx+a2-1≤0的解集为[-1，+∞），
∴a=0，
∴bx-1≤0；
即bx≤1，
∴b=-1；
综上，a=0，b=-1．
∴a=0，
∴bx-1≤0；
即bx≤1，
∴b=-1；
综上，a=0，b=-1．
点评：本题考查了不等式的解法与应用的问题，是基础题目．
练习册系列答案
阅读快车系列答案
相关题目
∫-10（x-ex）dx=（ ）
A、-1-
| ||||
| B、-1 | ||||
C、-
| ||||
D、-
|
函数f（x）是奇函数，且在（0，+∞）上是增函数，函数g（x）是偶函数，且在（0，+∞）上是减函数，那么在（-∞，0）上，它们的增减性是（ ）
| A、f（x）是减函数，g（x）是增函数 |
| B、f（x）是增函数，g（x）是减函数 |
| C、f（x）是减函数，g（x）是减函数 |
| D、f（x）是增函数，g（x）是增函数 |
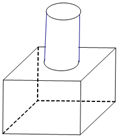某机器零件是如图所示的几何体（实心），零件下面是边长为10cm的正方体，上面是底面直径为4cm，高为10cm的圆柱．
若变量x，y满足约束条件
，则z=2x+y的最大值是（ ）
|
| A、2 | B、4 | C、5 | D、6 |