题目内容
14.南北朝时期我国数学著作《张丘建算经》有一道题为:“今有十等人,每等一人,宫赐金以等次差降之,上三人先入,的金四斤,持出,下四人后入得金三斤,持出,中间三人未到者,亦依等次更给,问各得金几何?”则在该问题中,等级较高的二等人所得黄金比等级较低的八等人和九等人两人所得黄金之和( )| A. | 多$\frac{7}{12}$斤 | B. | 少$\frac{7}{12}$斤 | C. | 多$\frac{1}{6}$斤 | D. | 少$\frac{1}{6}$斤 |
分析 设这十等人所得黄金的重量从大到小依次组成等差数列{an},则a1+a2+a3=4,a7+a8+a9+a10=3,由此利用等差数列的性质能求出结果.
解答 解:设这十等人所得黄金的重量从大到小依次组成等差数列{an},
则a1+a2+a3=4,a7+a8+a9+a10=3,
由等差数列的性质得${a}_{2}=\frac{4}{3}$,${a}_{8}+{a}_{9}=\frac{3}{2}$,
∴a2-(a8+a9)=$\frac{4}{3}-\frac{3}{2}$=-$\frac{1}{6}$.
∴级较高的二等人所得黄金比等级较低的八等人和九等人两人所得黄金之和少$\frac{1}{6}$斤.
故选:D.
点评 本题考查等差数列的性质,考查推理论证能力、运算求解能力,考查化归转化思想,是基础题.

练习册系列答案
相关题目
18.对于实数a>0,“$\frac{1}{x}$<a”是“x>$\frac{1}{a}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.已知k∈R,点P(a,b)是直线x+y=2k与圆x2+y2=k2-2k+3的公共点,则ab的最大值为( )
| A. | 15 | B. | 9 | C. | 1 | D. | -$\frac{5}{3}$ |
19.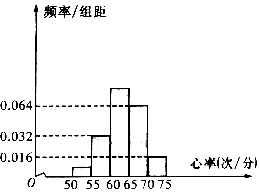 某学校的特长班有50名学生,其中有体育生20人,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75),按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.
某学校的特长班有50名学生,其中有体育生20人,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75),按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.
(1)求a的值,并求这50名学生心率的平均数;
(2)因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若从第一组和第二组的学生中随机抽取一名,该学生是体育生的概率为0.8,请将下面的列联表补充完整,并判断是否有99.5%的把握认为心率小于60次/分与常年进行系统的身体锻炼有关?请说明理由.
参考数据:
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
 某学校的特长班有50名学生,其中有体育生20人,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75),按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.
某学校的特长班有50名学生,其中有体育生20人,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75),按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.(1)求a的值,并求这50名学生心率的平均数;
(2)因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若从第一组和第二组的学生中随机抽取一名,该学生是体育生的概率为0.8,请将下面的列联表补充完整,并判断是否有99.5%的把握认为心率小于60次/分与常年进行系统的身体锻炼有关?请说明理由.
参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 心率小于60次/分 | 心率不小于60次/分 | 合计 | |
| 体育生 | 8 | 12 | 20 |
| 艺术生 | 2 | 28 | 30 |
| 合计 | 10 | 40 | 50 |
3.如表示意某科技公司2012~2016年年利润y(单位:十万元)与年份代号x之间的关系,如果该公司盈利变化规律保持不变,则第n年(以2012年为第1年)年利润的预报值是y=2n2-n.(直接写出代数式即可,不必附加单位)
| 年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年份代号x | 1 | 2 | 3 | 4 | 5 |
| 年利润/十万元 | 1 | 6 | 15 | 28 | 45 |
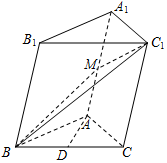 在斜三棱柱ABC-A1B1C1中,AB=AC,平面BB1C1C⊥底面ABC,点M、D分别是线段AA1、BC的中点.
在斜三棱柱ABC-A1B1C1中,AB=AC,平面BB1C1C⊥底面ABC,点M、D分别是线段AA1、BC的中点.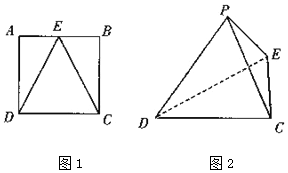 如图1,2,E是正方形ABCD的AB边的中点,将△AED与△BEC分别沿ED、EC折起,使得点A与点B重合,记为点P,得到三棱锥P-CDE.
如图1,2,E是正方形ABCD的AB边的中点,将△AED与△BEC分别沿ED、EC折起,使得点A与点B重合,记为点P,得到三棱锥P-CDE.