题目内容
11.已知定义在区间(0,+∞)上的函数f(x)满足f($\frac{{x}_{1}}{{x}_{2}}$)=f(x1)-f(x2).(1)求f(1)的值;
(2)若当x>1时,有f(x)<0.求证:f(x)为单调递减函数;
(3)在(2)的条件下,若f(5)=-1,求f(x)在[3,25]上的最小值.
分析 (1)利用赋值法进行求解.
(2)根据函数单调性的定义进行证明.
(3)根据函数单调性和抽象函数的关系进行转化求解即可.
解答 解:(1)令x1=x2>0,
代入得f(1)=f(x1)-f(x1)=0,
故f(1)=0.…(4分)
(2)证明:任取x1,x2∈(0,+∞),且x1>x2,则$\frac{{x}_{1}}{{x}_{2}}$>1,
由于当x>1时,f(x)<0,所以f($\frac{{x}_{1}}{{x}_{2}}$)<0,
即f(x1)-f(x2)<0,因此f(x1)<f(x2),
所以函数f(x)在区间(0,+∞)上是单调递减函数.…(8分)
(3)因为f(x)在(0,+∞)上是单调递减函数,
所以f(x)在[3,25]上的最小值为f(25).
由f($\frac{{x}_{1}}{{x}_{2}}$)=f(x1)-f(x2)得,
f(5)=f($\frac{25}{5}$)=f(25)-f(5),而f(5)=-1,
所以f(25)=-2.
即f(x)在[3,25]上的最小值为-2.…(12分)
点评 本题主要考查抽象函数的应用,利用赋值法以及函数单调性的定义是解决本题的关键.

练习册系列答案
相关题目
6.为了得到函数y=$\sqrt{2}$sin3x的图象,可以将函数y=$\sqrt{2}$sin(3x+$\frac{π}{2}$)的图象( )
| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{2}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向左平移$\frac{π}{2}$个单位 |
3.(log227)•(log34)=( )
| A. | $\frac{1}{6}$ | B. | 2 | C. | 3 | D. | 6 |
20.已知焦点在x轴上的椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{9}$=1的离心率e=$\frac{1}{2}$,则m=( )
| A. | 12 | B. | 18 | C. | $\frac{27}{4}$ | D. | 12或$\frac{27}{4}$ |
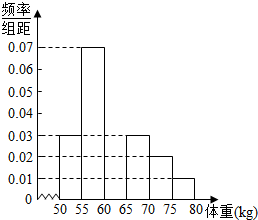 某校对高二年段的男生进行体检,现将高二男生的体重(kg)数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组[60,65)的人数为200.根据一般标准,高二男生体重超过65kg属于偏胖,低于55kg属于偏瘦.观察图形的信息,回答下列问题:
某校对高二年段的男生进行体检,现将高二男生的体重(kg)数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组[60,65)的人数为200.根据一般标准,高二男生体重超过65kg属于偏胖,低于55kg属于偏瘦.观察图形的信息,回答下列问题:
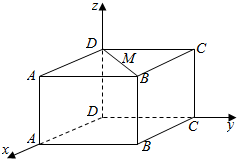 在如图所示的长方体ABCD-A1B1C1D1中,|DA|=8,|DC|=6,|DD1|=3,则D1B1的中点M的坐标为(4,3,3),|DM|=$\sqrt{34}$.
在如图所示的长方体ABCD-A1B1C1D1中,|DA|=8,|DC|=6,|DD1|=3,则D1B1的中点M的坐标为(4,3,3),|DM|=$\sqrt{34}$.