题目内容
2.(x2+a)(x-1)9的展开式中x3的系数为-159,则实数a=-2.分析 根据(x-1)9展开式的通项公式求出展开式中含x与x3项系数,即可求出(x2+a)(x-1)9的展开式中x3的系数.
解答 解:(x-1)9展开式的通项公式为:
Tr+1=${C}_{9}^{r}$•x9-r•(-1)r,
分别令9-r=1和3,可得r=8和6;
所以(x2+a)(x-1)9的展开式中x3的系数为:
${C}_{9}^{8}$•(-1)8+a•${C}_{9}^{6}$•(-1)6=-159,
即9+84a=-159,
解得a=-2.
故答案为:-2.
点评 本题考查了二项式定理的应用问题,也考查了推理能力与计算能力,是基础题目.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
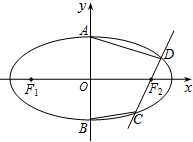 已知F1,F2分别是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左,右焦点,A,B分别为椭圆的上,下顶点.过椭圆的右焦点F2的直线在y轴右侧交椭圆于C,D两点.△F1CD的周长为8,且直线AC,BC的斜率之积为$-\frac{1}{4}$.
已知F1,F2分别是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左,右焦点,A,B分别为椭圆的上,下顶点.过椭圆的右焦点F2的直线在y轴右侧交椭圆于C,D两点.△F1CD的周长为8,且直线AC,BC的斜率之积为$-\frac{1}{4}$.