题目内容
为防止山体滑坡,某地决定建设既美化又防护的绿化带,种植松树、柳树等植物.某人一次种植了n株柳树,各株柳树成活与否是相互独立的,成活率为p,设ξ为成活柳树的株数,数学期望E(ξ)=3,标准差σ(ξ)为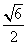 .
.
(1) 求n、p的值并写出ξ的分布列;
(2) 若有3株或3株以上的柳树未成活,则需要补种,求需要补种柳树的概率.
解:(1) 由E(ξ)=np=3,(σ(ξ))2=np(1-p)=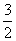 ,得1-p=
,得1-p=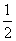 ,从而n=6,p=
,从而n=6,p=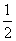 ,
,
ξ的分布列为
| ξ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| P |
|
|
|
|
|
|
|

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
(2013·天津)某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.先从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
| 产品编号 | A1 | A2 | A3 | A4 | A5 |
| 质量指标(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
| 产品编号 | A6 | A7 | A8 | A9 | A10 |
| 质量指标(x,y,z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(1) 利用上表提供的样本数据估计该批产品的一等品率;
(2) 在该样品的一等品中,随机抽取两件产品,
① 用产品编号列出所有可能的结果;
② 设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率.

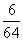

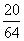
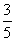
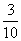
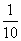
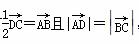 ,则这个四边形是________.
,则这个四边形是________.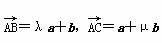 (λ、μ∈R),当A、B、C三点共线时λ、μ满足的条件为________.
(λ、μ∈R),当A、B、C三点共线时λ、μ满足的条件为________.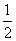 ,则
,则 =________.
=________.