题目内容
20.已知向量$\overrightarrow a$与$\overrightarrow b$的夹角为60,$|{\overrightarrow a}|=4,|{\overrightarrow b}|=1,则\overrightarrow b⊥(\overrightarrow a-x•\overrightarrow b)$时,实数x为( )| A. | 4 | B. | 2 | C. | l | D. | $\frac{1}{2}$ |
分析 利用两个向量的数量积的定义,两个向量垂直的性质,求得实数x的值.
解答 解:∵向量$\overrightarrow a$与$\overrightarrow b$的夹角为60°,$|{\overrightarrow a}|=4,|{\overrightarrow b}|=1,则\overrightarrow b⊥(\overrightarrow a-x•\overrightarrow b)$时,
∴$\overrightarrow{a}•\overrightarrow{b}$-x•${\overrightarrow{b}}^{2}$=4•1•cos60°-x=0,求得x=2,
故选:B.
点评 本题主要考查两个向量的数量积的定义,两个向量垂直的性质,属于基础题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
10.在复平面中,复数$\frac{1}{(1+i)^{2}+1}$对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.已知正项等差数列{an}中,a1+a2+a3=15,若a1+2,a2+5,a3+13成等比数列,则a10=( )
| A. | 21 | B. | 22 | C. | 23 | D. | 24 |
8.已知实数x、y满足约束条件$\left\{\begin{array}{l}{x-y+1≥0}\\{2x+y-a≥0}\\{2x-y-4≤0}\end{array}\right.$,若z=$\frac{y+1}{x+1}$的最小值为-$\frac{1}{4}$,则正数a的值为( )
| A. | $\frac{7}{6}$ | B. | 1 | C. | $\frac{3}{4}$ | D. | $\frac{8}{9}$ |
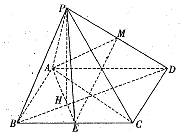 四棱锥P-ABCD中,底面ABCD为矩形,$AB=2,BC=2\sqrt{2},E$为BC的中点,连接AE,BD,交点H,PH⊥平面ABCD,M为PD的中点.
四棱锥P-ABCD中,底面ABCD为矩形,$AB=2,BC=2\sqrt{2},E$为BC的中点,连接AE,BD,交点H,PH⊥平面ABCD,M为PD的中点. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形ABCD满足AB⊥AD,BC∥AD且BC=4,点M为PC中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形ABCD满足AB⊥AD,BC∥AD且BC=4,点M为PC中点.