题目内容
函数f(x)是定义在R上的偶函数,f(0)=0,当x>0时,f(x)=lo
x.
(1)求函数f(x)的解析式.
(2)解不等式f(x2-1)>-2.
解:(1)当x<0时,-x>0,则f(-x)=lo(-x).
因为函数f(x)是偶函数,所以f(-x)=f(x).
所以函数f(x)的解析式为
f(x)=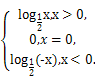
(2)因为f(4)=lo4=-2,f(x)是偶函数,
所以不等式f(x2-1)>-2可化为f(|x2-1|)>f(4).
又因为函数f(x)在(0,+∞)上是减函数,
所以|x2-1|<4,解得-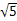
<x<,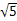
即不等式的解集为(-,).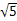
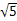练习册系列答案
相关题目
(2x+1)(1≤x≤3)的值域为 . 
)2.5,则a,b,c的大小关系是( )
) (C)(
若f(a)=
+
的最小值是 . 
)的导数是( )
) (D)f′(x)=2sin(4x+