题目内容
3.将函数y=$\sqrt{3}$cos2x-sin2x的图象向右平移$\frac{π}{3}$个单位长度,所得图象对应的函数为g(x),则g(x)=( )| A. | -2sin2x | B. | 2sin2x | C. | 2cos(2x-$\frac{π}{6}$) | D. | 2sin(2x-$\frac{π}{6}$) |
分析 由两角和的余弦函数公式化简函数,再由图象平移的规律即可得解.
解答 解:化简函数得y=$\sqrt{3}$cos2x-sin2x=2cos(2x+$\frac{π}{6}$),
所以将函数的图象向右平移$\frac{π}{3}$个单位长度,
所得图象对应的函数g(x)=2cos[2(x-$\frac{π}{3}$)+$\frac{π}{6}$]=2sin2x.
故选:B.
点评 本题考查三角函数的化简和图象变换,属于中档题.

练习册系列答案
相关题目
2.已知α是第二象限角,且tanα=-$\frac{1}{3}$,则sin2α=( )
| A. | -$\frac{3\sqrt{10}}{10}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | -$\frac{3}{5}$ | D. | $\frac{3}{5}$ |
14.已知直线l1:$\frac{x}{m-2}$-$\frac{4m}{m-2}$y+2=0,l2:m2x+$\frac{y}{m}$-9=0.若l1⊥l2,则m的值是( )
| A. | -$\frac{1}{2}$ | B. | -2 | C. | $\frac{1}{2}$ | D. | 2 |
11.下列函数中最小值为4的是( )
| A. | $y=x+\frac{4}{x}$ | B. | y=3x+4•3-x | ||
| C. | $y=sinx+\frac{4}{sinx}$ (0<x<π) | D. | y=lgx+4logx10 |
15.若实数x,y满足约束条件$\left\{\begin{array}{l}{y≤1}\\{x+y≥0}\\{x-y-2≤0}\end{array}\right.$,则z=2x-y的最大值为( )
| A. | 4 | B. | 5 | C. | 2 | D. | 1 |
12.在△ABC中,两直角边和斜边分别为a,b,c,若a+b=cx,试确定实数x的取值范围( )
| A. | $({1,\sqrt{2}}]$ | B. | $({0,\sqrt{2}}]$ | C. | $[{\sqrt{2},2})$ | D. | $[{\sqrt{2},\sqrt{3}}]$ |
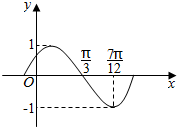 函数f(x)=sin(ωx+φ)(ω>0,|φ|>$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=sin(ωx+φ)(ω>0,|φ|>$\frac{π}{2}$)的部分图象如图所示.