题目内容
已知椭圆两焦点的坐标分别是（-2，0），（2，0），并且经过点（2，
），求椭圆方程．
| 2 |
考点：椭圆的标准方程
专题：圆锥曲线的定义、性质与方程
分析：直接根据焦点的坐标设出椭圆的方程，再根据点的坐标求出结果．
解答：
解：椭圆两焦点的坐标分别是（-2，0），（2，0），
所以：设椭圆的方程为：
+
=1(a＞b＞0)
由于：椭圆经过点（2，
），
则：
+
=1，
且a2=b2+4，
则：
，
解得：
．
椭圆方程为：
+
=1．
所以：设椭圆的方程为：
| x2 |
| a2 |
| y2 |
| b2 |
由于：椭圆经过点（2，
| 2 |
则：
| 4 |
| a2 |
| 2 |
| b2 |
且a2=b2+4，
则：
|
解得：
|
椭圆方程为：
| x2 |
| 8 |
| y2 |
| 4 |
点评：本题考查的知识要点：椭圆方程的求法，属于基础题型．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
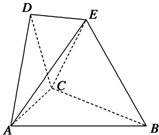在如图所示的空间几何体中，平面ACD⊥平面ABC，△ACD与△ACB是边长为2的等边三角形，BE=2，BE和平面ABC所成的角为60°，且点E在平面ABC上的射影落在∠ABC的平分线上．
如图，△ABC为正三角形，EC⊥平面ABC，BD⊥平面ABC，CE=CA=2BD，M是EA的中点，N是EC的中点，求证：平面DMN∥平面ABC．