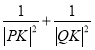题目内容
【题目】已知四面体
的所有顶点在球
的表面上，
平面
，
，
，则球的表面积为_________.
【答案】
【解析】
将四面体补成直三棱柱
，根据题意画出图象，设
，
的外心分别为
，
，则点
为线段
的中点，求出
，在根据正弦定理，求出
，根据勾股定理和球的表面积公式，即可求得答案.
四面体
的所有顶点在球的表面上，且
平面
，
将四面体补成直三棱柱，
设，的外心分别为，，则点为线段的中点，
根据直棱柱特征可得：
面
根据题意画出图象，如图：
[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/18/2487522753945600/2488179565330432/EXPLANATION/6f612c2d35a74b139ecb71f4a35bdeaa.png]
可得：
，
在根据正弦定理：
(
为三角形外接圆半径)
根据为的外心，可得为外接圆半径
即
，
面，
面
故
为直角三角形
在
中，根据勾股定理可得：
，
.
故答案为：.
练习册系列答案
相关题目
