题目内容
如果函数 的定义域为R,对于定义域内的任意
的定义域为R,对于定义域内的任意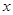 ,存在实数
,存在实数 使得
使得 成立,则称此函数具有“
成立,则称此函数具有“ 性质”。
性质”。
(1)判断函数 是否具有“
是否具有“ 性质”,若具有“
性质”,若具有“ 性质”,求出所有
性质”,求出所有 的值;若不具有“
的值;若不具有“ 性质”,说明理由;
性质”,说明理由;
(2)已知 具有“
具有“ 性质”,且当
性质”,且当 时
时 ,求
,求 在
在 上有最大值;
上有最大值;
(3)设函数 具有“
具有“ 性质”,且当
性质”,且当 时,
时, .若
.若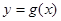 与
与 交点个数为2013,求
交点个数为2013,求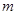 的值.
的值.
(1)  ,(2) 当
,(2) 当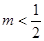 时,
时,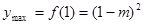 ,当
,当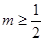 时,
时, , (3)
, (3)  .
.
解析试题分析:(1)新定义问题,必须从定义出发,实际是对定义条件的直译. 由 得
得 ,(2)由
,(2)由  性质知函数为偶函数. ∴
性质知函数为偶函数. ∴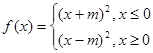 当
当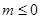 时,∵
时,∵ 在
在 单调增,∴
单调增,∴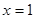 时,
时, ,当
,当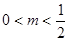 时,∵
时,∵ 在
在 单调减,在
单调减,在 上单调增,又
上单调增,又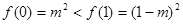 ,∴
,∴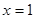 时,
时, ,当
,当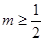 时,∵
时,∵ 在
在 单调减,在
单调减,在 上单调增,又
上单调增,又 ,∴
,∴ 时,
时,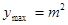 . (3) ∵函数
. (3) ∵函数 具有“
具有“ 性质” ∴
性质” ∴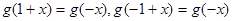 ∴
∴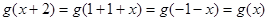 ∴函数
∴函数 是以2为周期的函数. 当
是以2为周期的函数. 当 时,
时, 为偶函数,因此易得函数
为偶函数,因此易得函数 是以1为周期的函数.结合图像得: ①当
是以1为周期的函数.结合图像得: ①当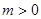 时,要使得
时,要使得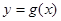 与
与 有2013个交点,只要
有2013个交点,只要 与
与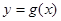 在区间
在区间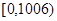 有2012个交点,而在
有2012个交点,而在 内有一个交点∴
内有一个交点∴ 过
过 ,从而得
,从而得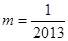 ,②当
,②当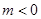 时,同理可得
时,同理可得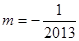 ,③当
,③当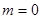 时,不合题意, 综上所述
时,不合题意, 综上所述 .
.
(1)由 得
得
∴
∴函数 具有“
具有“ 性质”,其中
性质”,其中 2分
2分
(2) ∵ 具有“
具有“ 性质”
性质”
∴
设 ,则
,则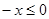 ,∴
,∴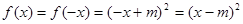
∴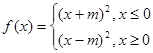 4分
4分
当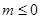 时,∵
时,∵ 在
在 单调增,∴
单调增,∴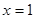 时,
时, 5分
5分
当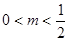 时,∵
时,∵ 在
在 单调减,在
单调减,在 上单调增
上单调增
又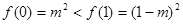 ,∴
,∴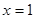 时,
时,
练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
 ,
, .
. ,使
,使 ;
; ,使
,使 ,且对(1)中的
,且对(1)中的 .
. .
. ),f(
),f( )是否成等比数列,并证明f(
)是否成等比数列,并证明f( 为a、b的调和平均数,记为H.若H≤f(x)≤G,求x的取值范围.
为a、b的调和平均数,记为H.若H≤f(x)≤G,求x的取值范围.
 ,其中
,其中 ,
, 为正整数,
为正整数, ,
, ,
, 均为常数,曲线
均为常数,曲线 在
在 处的切线方程为
处的切线方程为 .
. 的最大值;
的最大值; 都有
都有 .(
.( 为自然对数的底)
为自然对数的底) .
.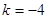 时,求函数
时,求函数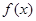 在
在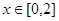 上的值域;
上的值域; ,若存在
,若存在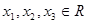 ,使得以
,使得以 为三边长的三角形不存在,求实数
为三边长的三角形不存在,求实数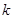 的取值范围.
的取值范围. ,
,
 ,函数
,函数 的图像与直线
的图像与直线 的相邻两个交点之间的距离为
的相邻两个交点之间的距离为 .
. 的值;
的值;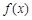 在
在 上的单调递增区间.
上的单调递增区间.
 .
. 的单调区间和极值;
的单调区间和极值; 对
对 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.