题目内容
已知 ,
, .
.
(1)求 的值;
的值;
(2)求函数 的值域.
的值域.
(1) ,(2)
,(2) .
.
解析试题分析:(1)本题有两个化简方向,一是展开,利用同角三角函数关系求角,即 ,结合
,结合 解得
解得 ,二是利用角的关系,即
,二是利用角的关系,即
 (2)研究函数性质,首先化为一元函数,即利用二倍角公式化简得:
(2)研究函数性质,首先化为一元函数,即利用二倍角公式化简得:

 ,因为
,因为 ,所以值域为
,所以值域为 .
.
试题解析:(1)因为 ,且
,且 ,所以
,所以 ,
, .
.
因为
 .所以
.所以 . 6
. 6
(2)由(1)可得 . 所以
. 所以

 ,
, . 因为
. 因为 ,所以,当
,所以,当 时,
时, 取最大值
取最大值 ;当
;当 时,
时, 取最小值
取最小值 .
.
所以函数 的值域为
的值域为 . 14分
. 14分
考点:给值求值,函数值域

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 ,
,
 ,函数
,函数 的图像与直线
的图像与直线 的相邻两个交点之间的距离为
的相邻两个交点之间的距离为 .
. 的值;
的值;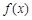 在
在 上的单调递增区间.
上的单调递增区间. ,用
,用 表示
表示 当
当 时的函数值中整数值的个数.
时的函数值中整数值的个数. ,求
,求 .
. ,若
,若 ,求
,求 的最小值.
的最小值. 的定义域为E,值域为F.
的定义域为E,值域为F. 与集合F的关系;
与集合F的关系; },求实数a的值.
},求实数a的值. ,F=[2﹣3m,2﹣3n],求m,n的值.
,F=[2﹣3m,2﹣3n],求m,n的值. 在点
在点 处的切线方程为
处的切线方程为
 .
. 、
、 的值;
的值;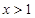 时,
时, 恒成立,求实数
恒成立,求实数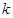 的取值范围;
的取值范围; ,且
,且 时,
时, .
.
 .
. 的单调区间和极值;
的单调区间和极值; 对
对 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围. -
- +1的最小值与最大值.
+1的最小值与最大值.