题目内容
已函数 .
.
(1)作出函数 的图像;
的图像;
(2)若对任意 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)函数 的图像详见解析;(2)实数
的图像详见解析;(2)实数 的取值范围为
的取值范围为 .
.
解析试题分析:(1)用零点分段法分: 、
、 、
、 三种情况化简函数
三种情况化简函数 ,从而得到
,从而得到
 ,再根据一次函数的图像作法作出函数
,再根据一次函数的图像作法作出函数 的图像即可;(2)依题意先将问题转化为
的图像即可;(2)依题意先将问题转化为 ,借用(1)中函数
,借用(1)中函数 的图像求出最低点的纵坐标即函数
的图像求出最低点的纵坐标即函数 的最小值4,最后求解二次不等
的最小值4,最后求解二次不等 即可得到
即可得到 的取值范围.
的取值范围.
试题解析:(1)①当 时,
时,
②当 时,
时,
③当 时,
时,
∴

∴ 的图象如图所示
的图象如图所示
(2)由(1)知 的最小值为4,由题意可知
的最小值为4,由题意可知
即 ,即
,即 ,解得
,解得
故实数 的取值范围为
的取值范围为 .
.
考点:1.函数的图像;2.函数的最值;3.二次不等式.

练习册系列答案
相关题目
 (x≠a).
(x≠a).
 ,其中
,其中 ,
, 为正整数,
为正整数, ,
, ,
, 均为常数,曲线
均为常数,曲线 在
在 处的切线方程为
处的切线方程为 .
. 的最大值;
的最大值; 都有
都有 .(
.( 为自然对数的底)
为自然对数的底) ,其
,其 中为常数,
中为常数, .
. 时,求曲线
时,求曲线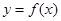 在点
在点 处的切线方程;
处的切线方程; 的极大值为
的极大值为 ?若存在,求出
?若存在,求出 ,
,
 ,函数
,函数 的图像与直线
的图像与直线 的相邻两个交点之间的距离为
的相邻两个交点之间的距离为 .
. 的值;
的值;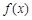 在
在 上的单调递增区间.
上的单调递增区间. ,用
,用 表示
表示 当
当 时的函数值中整数值的个数.
时的函数值中整数值的个数. ,求
,求 .
. ,若
,若 ,求
,求 的最小值.
的最小值. 在点
在点 处的切线方程为
处的切线方程为
 .
. 、
、 的值;
的值;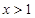 时,
时, 恒成立,求实数
恒成立,求实数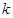 的取值范围;
的取值范围; ,且
,且 时,
时, .
. ,试求函数的零点个数.
,试求函数的零点个数.