题目内容
椭圆的一个顶点是(0,2),离心率为 ,坐标轴为对称轴的椭圆的标准方程为
,坐标轴为对称轴的椭圆的标准方程为
- A.
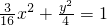
- B.
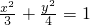
- C.
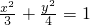 或
或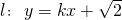
- D.
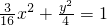 或
或 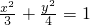
D
分析:分焦点在x轴与焦点在y轴讨论即可求得答案.
解答:当焦点在x轴,由题意得,b=2,
∵e2= =
=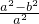 =
= =
= ,
,
∴a2= ,
,
∴椭圆的方程为: x2+
x2+ =1;
=1;
当焦点在y轴,同理可求得a=2,b= ,
,
∴椭圆的方程为: +
+ =1.
=1.
故选D.
点评:本题考查椭圆的标准方程与椭圆的几何性质,考查分类讨论思想与方程思想,属于中档题.
分析:分焦点在x轴与焦点在y轴讨论即可求得答案.
解答:当焦点在x轴,由题意得,b=2,
∵e2=
 =
=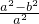 =
= =
= ,
,∴a2=
 ,
,∴椭圆的方程为:
 x2+
x2+ =1;
=1;当焦点在y轴,同理可求得a=2,b=
 ,
,∴椭圆的方程为:
 +
+ =1.
=1.故选D.
点评:本题考查椭圆的标准方程与椭圆的几何性质,考查分类讨论思想与方程思想,属于中档题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
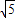 ),离心率为
),离心率为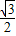
 x+m与椭圆相交于A、B两点,椭圆的左右焦点分别是F1和F2,求:以F1F2和AB为对角线的四边形F1AF2B面积的最大值.
x+m与椭圆相交于A、B两点,椭圆的左右焦点分别是F1和F2,求:以F1F2和AB为对角线的四边形F1AF2B面积的最大值.