题目内容
已知:中心在原点,长轴在x轴上的椭圆的一个顶点是(0,-
),离心率为
(1)求:椭圆方程;(2)若直线y=
x+m与椭圆相交于A、B两点,椭圆的左右焦点分别是F1和F2,求:以F1F2和AB为对角线的四边形F1AF2B面积的最大值.
| 5 |
| ||
| 2 |
(1)求:椭圆方程;(2)若直线y=
| 1 |
| 2 |
(1)设中心在原点,长轴在x轴上的椭圆方程:
+
=1(a>b>0)
∵椭圆的一个顶点是(0,-
)∴b=
∵离心率为e=
=
c=
a
∵a2=b2+c2,∴a2=20,b2=5
∴椭圆方程:
+
=1
(2)椭圆方程:
+
=1
∴左右焦点为F1(-
,0),F2(
,0),F1F2=2
联立方程
整理可得,2y2-2my+m2-5=0
∵直线与椭圆相交于A、B两点,∴△=4m2-8(m2-5)>0,即:-
<m<
,且y1+y2=m,y1y2=
由题知:以F1F2和AB为对角线的四边形F1AF2B面积S=
|F1F2||y1-y2|=2
×
=
≤5
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆的一个顶点是(0,-
| 5 |
| 5 |
∵离心率为e=
| c |
| a |
| ||
| 2 |
| ||
| 2 |
∵a2=b2+c2,∴a2=20,b2=5
∴椭圆方程:
| x2 |
| 20 |
| y2 |
| 5 |
(2)椭圆方程:
| x2 |
| 20 |
| y2 |
| 5 |
∴左右焦点为F1(-
| 15 |
| 15 |
| 15 |
联立方程
|
∵直线与椭圆相交于A、B两点,∴△=4m2-8(m2-5)>0,即:-
| 10 |
| 10 |
| m2-5 |
| 2 |
由题知:以F1F2和AB为对角线的四边形F1AF2B面积S=
| 1 |
| 2 |
| 15 |
| (y1+y2)2-4y1y2 |
| 1 |
| 2 |
| 15 |
| 10-m2 |
| 6 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
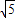 ),离心率为
),离心率为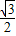
 x+m与椭圆相交于A、B两点,椭圆的左右焦点分别是F1和F2,求:以F1F2和AB为对角线的四边形F1AF2B面积的最大值.
x+m与椭圆相交于A、B两点,椭圆的左右焦点分别是F1和F2,求:以F1F2和AB为对角线的四边形F1AF2B面积的最大值.