题目内容
已知:中心在原点,长轴在x轴上的椭圆的一个顶点是(0,-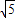 ),离心率为
),离心率为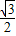
(1)求:椭圆方程;(2)若直线y=
 x+m与椭圆相交于A、B两点,椭圆的左右焦点分别是F1和F2,求:以F1F2和AB为对角线的四边形F1AF2B面积的最大值.
x+m与椭圆相交于A、B两点,椭圆的左右焦点分别是F1和F2,求:以F1F2和AB为对角线的四边形F1AF2B面积的最大值.
【答案】分析:(1)设中心在原点,长轴在x轴上的椭圆方程: (a>b>0),由椭圆的一个顶点可求b,由离心率为
(a>b>0),由椭圆的一个顶点可求b,由离心率为 可得a,c的关系,结合a2=b2+c2,可求a,b,c进而可求椭圆的方程
可得a,c的关系,结合a2=b2+c2,可求a,b,c进而可求椭圆的方程
(2)由(1)可得椭圆方程 ,联立方程
,联立方程 整理可得,2y2-2my+m2-5=0,由直线与椭圆相交于A、B两点,可得△=4m2-8(m2-5)>0,及
整理可得,2y2-2my+m2-5=0,由直线与椭圆相交于A、B两点,可得△=4m2-8(m2-5)>0,及 ,而以F1F2和AB为对角线的四边形F1AF2B面积
,而以F1F2和AB为对角线的四边形F1AF2B面积 可求
可求
解答:解:(1)设中心在原点,长轴在x轴上的椭圆方程: (a>b>0)
(a>b>0)
∵椭圆的一个顶点是 ∴
∴
∵离心率为

∵a2=b2+c2,∴a2=20,b2=5
∴椭圆方程:
(2)椭圆方程:
∴左右焦点为 ,
, ,
,
联立方程 整理可得,2y2-2my+m2-5=0
整理可得,2y2-2my+m2-5=0
∵直线与椭圆相交于A、B两点,∴△=4m2-8(m2-5)>0,即: ,且
,且
由题知:以F1F2和AB为对角线的四边形F1AF2B面积 =
= ×
× =
=

点评:本题主要考查了由椭圆的性质求解椭圆方程,直线与椭圆的位置关系的应用,体现了方程的思想的应用,要注意弦长公式| 的应用.
的应用.
 (a>b>0),由椭圆的一个顶点可求b,由离心率为
(a>b>0),由椭圆的一个顶点可求b,由离心率为 可得a,c的关系,结合a2=b2+c2,可求a,b,c进而可求椭圆的方程
可得a,c的关系,结合a2=b2+c2,可求a,b,c进而可求椭圆的方程(2)由(1)可得椭圆方程
 ,联立方程
,联立方程 整理可得,2y2-2my+m2-5=0,由直线与椭圆相交于A、B两点,可得△=4m2-8(m2-5)>0,及
整理可得,2y2-2my+m2-5=0,由直线与椭圆相交于A、B两点,可得△=4m2-8(m2-5)>0,及 ,而以F1F2和AB为对角线的四边形F1AF2B面积
,而以F1F2和AB为对角线的四边形F1AF2B面积 可求
可求解答:解:(1)设中心在原点,长轴在x轴上的椭圆方程:
 (a>b>0)
(a>b>0)∵椭圆的一个顶点是
 ∴
∴
∵离心率为


∵a2=b2+c2,∴a2=20,b2=5
∴椭圆方程:

(2)椭圆方程:

∴左右焦点为
 ,
, ,
,
联立方程
 整理可得,2y2-2my+m2-5=0
整理可得,2y2-2my+m2-5=0∵直线与椭圆相交于A、B两点,∴△=4m2-8(m2-5)>0,即:
 ,且
,且
由题知:以F1F2和AB为对角线的四边形F1AF2B面积
 =
= ×
× =
=

点评:本题主要考查了由椭圆的性质求解椭圆方程,直线与椭圆的位置关系的应用,体现了方程的思想的应用,要注意弦长公式|
 的应用.
的应用. 
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目