Question

半球内有一个内接正方体，正方体的一个面在半球的底面圆内，若正方体棱长为

6

，求球的表面积和体积．

Answer 1

考点：球的体积和表面积

专题：空间位置关系与距离

分析：根据题意，球心O为正方体的底面ABCD的中心，由正方体的性质与勾股定理算出球半径R=3，再利用球的表面积和体积公式加以计算，可得该半球的表面积和体积．

解答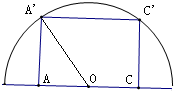： 解：设正方形ABCD-A'B'C'D'的底面ABCD在半球的底面圆上，如图
则球心O为ABCD的中心，连结OA'
∵正方体的棱长为

6

，
∴A0=

1

2

A′C′=

1

2

×

2

×

6

=

3

，可得A'O=

AA′2+AO2

=

6+3

=3，
即半球的半径R=3，
因此，半球的表面积为

1

2

×4×π×32=18π；
体积V=

1

2

×

4

3

×π×33=18π．

点评：本题给出正方体内接于半球内，在已知正方体棱长的情况下求半球的体积，着重考查了正方体的性质、勾股定理和球的体积公式等知识，关键是通过正方体与球的关系得到球的半径为底面中心到上底面顶点的距离，考查了学生的空间想象能力，属于中档题．