题目内容
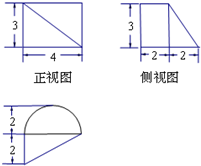
一个几何体的三视图如图所示，则该几何体的体积为 ．
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由三视图知几何体为半圆柱和直三棱柱，半圆柱的半径为2，高为3，体积为6π，直三棱柱的底面为直角三角形，面积为4，高为3，体积为12，可得几何体的体积．
解答：
解：由三视图知几何体为半圆柱和直三棱柱，半圆柱的半径为2，高为3，体积为6π，直三棱柱的底面为直角三角形，面积为4，高为3，体积为12，故几何体的体积为6π+12．
故答案为：6π+12．
故答案为：6π+12．
点评：本题考查了由三视图求几何体的体积，解题的关键是由三视图判断几何体的形状及数据所对应的几何量．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
设m，n是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题：
①若m⊥α，n∥α，则m⊥n；
②若m∥α，n∥α，则m∥n；
③若α∥β，β∥γ，m⊥α，则m⊥γ；
④若α⊥γ，β⊥γ，则α∥β；
其中正确命题的序号是（ ）
①若m⊥α，n∥α，则m⊥n；
②若m∥α，n∥α，则m∥n；
③若α∥β，β∥γ，m⊥α，则m⊥γ；
④若α⊥γ，β⊥γ，则α∥β；
其中正确命题的序号是（ ）
| A、①和③ | B、②和③ |
| C、②和④ | D、①和④ |
已知函数f（x）=
，则f（-10）的值是（ ）
|
| A、-2 | B、-1 | C、0 | D、1 |
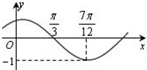函数f（x）=Acos（ωx+φ）（A＞0，ω＞0）的图象如图所示，为了得到g（x）=Acosωx的图象，可以将f（x）的图象（ ）A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
以直线x-2y=0和x+2y-4=0的交点为圆心，且过点（2，0）的圆的方程为（ ）
| A、（x-2）2+（y-1）2=1 |
| B、（x+2）2+（y+1）2=1 |
| C、（x-2）2+（y-1）2=2 |
| D、（x+2）2+（y+1）2=2 |