题目内容
16.以下是新兵训练时,某炮兵连8周中炮弹对同一目标的命中情况的柱状图: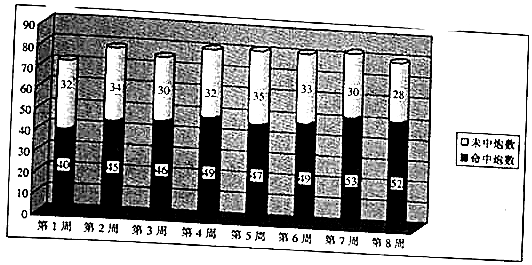
(1)计算该炮兵连这8周中总的命中频率p0,并确定第几周的命中频率最高;
(2)以(1)中的p0作为该炮兵连炮兵甲对同一目标的命中率,若每次发射相互独立,且炮兵甲发射3次,记命中的次数为X,求X的数学期望;
(3)以(1)中的p0作为该炮兵连炮兵对同一目标的命中率,试问至少要用多少枚这样的炮弹同时对该目标发射一次,才能使目标被击中的概率超过0.99?(取lg0.4=-0.398)
分析 (1)先求出这8周总总命中炮数和总未命中炮数,由此能求出该炮兵连这8周中总的命中频率,从而根据表中数据能求出第8周的命中率最高.
(2)由题意知X~B(3,0.6),由此能求出X的数学期望.
(3)由1-(1-P0)n>0.99,得0.4n<0.01,由此能求出至少要用6枚这样的炮弹同时对该目标发射一次,才能使目标被击中的概率超过0.99.
解答 解:(1)这8周总总命中炮数为:40+45+46+49+47+49+53+52=381,
总未命中炮数为32+34+30+32+35+33+30+28=254,
∴该炮兵连这8周中总的命中频率p0=$\frac{381}{381+254}=0.6$,
∵$\frac{52}{28}>\frac{53}{30}$,
∴根据表中数据知第8周的命中率最高.
(2)由题意知X~B(3,0.6),
则X的数学期望为E(X)=3×0.6=1.8.
(3)由1-(1-P0)n>0.99,解得0.4n<0.01,
∴n>log0.40.01=$\frac{lg0.01}{lg0.4}$=-$\frac{2}{lg0.4}$=$\frac{2}{0.398}$≈5.025,
∴至少要用6枚这样的炮弹同时对该目标发射一次,才能使目标被击中的概率超过0.99.
点评 本题考查频率的求法及应用,考查概率的求法及应用,是中档题,解题时要认真审题,注意二项分布的合理运用.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
10.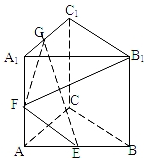 正三棱柱ABC-A1B1C1,E,F,G为 AB,AA1,A1C1的中点,则B1F与面GEF成角的正弦值( )
正三棱柱ABC-A1B1C1,E,F,G为 AB,AA1,A1C1的中点,则B1F与面GEF成角的正弦值( )
 正三棱柱ABC-A1B1C1,E,F,G为 AB,AA1,A1C1的中点,则B1F与面GEF成角的正弦值( )
正三棱柱ABC-A1B1C1,E,F,G为 AB,AA1,A1C1的中点,则B1F与面GEF成角的正弦值( )| A. | $\frac{5}{6}$ | B. | $\frac{3}{5}$ | C. | $\frac{3\sqrt{3}}{10}$ | D. | $\frac{3\sqrt{6}}{10}$ |
11.已知f(x)为奇函数,当x<0时,f(x)=a+x+log2(-x),其中a∈(-4,5),则f(4)>0的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
8.在平面直角坐标系中,方程$\frac{|x|}{2}$+$\frac{|y|}{4}$=1所表示的曲线是( )
| A. | 椭圆 | B. | 三角形 | C. | 菱形 | D. | 两条平行线 |
5.若集合A={y|y=lgx},B={x|y=$\sqrt{x}$},则集合A∩B=( )
| A. | (0,+∞) | B. | [0,+∞) | C. | (1,+∞) | D. | ∅ |
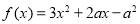 ,其中
,其中 ,
, 对任意的
对任意的 都成立,在1和
都成立,在1和 两数间插入2015个数,使之与1,
两数间插入2015个数,使之与1,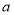 构成等比数列,设插入的这2015个数的成绩为
构成等比数列,设插入的这2015个数的成绩为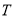 ,则
,则 ( )
( ) B.
B.
 D.
D.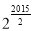
 .
. ,求证:
,求证: ;
; ,
, ,求
,求 的最大值;
的最大值; 时,
时, .
.