如图.位于A处前方有两个观察站B.D.且△ABD为边长等于3km的正三角形.当发现目标出现于C处时.测得∠BDC=45°.∠CBD=75°.则AC=( )A．15-6$\sqrt{3}$kmB．15+6$\sqrt{3}$kmC．$\sqrt{15+6\sqrt{3}}$kmD．$\sqrt{15-6\sqrt{3}}$km 题目和参考答案——青夏教育精英家教网—

题目内容

18．如图，位于A处前方有两个观察站B，D，且△ABD为边长等于3km的正三角形，当发现目标出现于C处时，测得∠BDC=45°，∠CBD=75°，则AC=（　　）

A．

15-6$\sqrt{3}$km

B．

15+6$\sqrt{3}$km

C．

$\sqrt{15+6\sqrt{3}}$km

D．

$\sqrt{15-6\sqrt{3}}$km

分析先利用正弦定理，求出DC，再用余弦定理，求出AC．

解答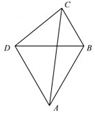解：由题意，∠BCD=60°，∴$\frac{3}{sin60°}$=$\frac{DC}{sin75°}$，
∴DC=$\frac{1}{2}$（3$\sqrt{2}$+$\sqrt{6}$），
∵∠CDA=105°，
∴AC=$\sqrt{（\frac{3\sqrt{2}+\sqrt{6}}{2}）^{2}+9-2•\frac{3\sqrt{2}+\sqrt{6}}{2}•3•（-\frac{\sqrt{6}+\sqrt{2}}{4}）}$=$\sqrt{15+6\sqrt{3}}$，
故选C．

点评本题考查正弦、余弦定理的运用，考查学生的计算能力，属于中档题．

练习册系列答案

相关题目

x	8	12	13	a	18
y	10	8	6	7	4

9．已知点M（a，b）在直线3x+4y-15=0上，则$\sqrt{（a-1）^{2}+（b+2）^{2}}$的最小值是4．

6．已知函数f（x）=ax³+x²（a∈R）在x=-$\frac{4}{3}$处取得极值．
（1）确定a的值和f（x）的极值；
（2）若g（x）=f（x）e^x，讨论g（x）的单调性．

13．柜子里有3双不同的鞋，随机地取2只，下列叙述错误的是（　　）

	A．	取出的鞋不成对的概率是$\frac{4}{5}$
	B．	取出的鞋都是左脚的概率是$\frac{1}{5}$
	C．	取出的鞋都是同一只脚的概率是$\frac{2}{5}$
	D．	取出的鞋一只是左脚的，一只是右脚的，但它们不成对的概率是$\frac{12}{25}$