题目内容
13.已知圆心为H的圆x2+y2+2x-15=0和定点A(1,0),B是圆上任意一点,线段AB的中垂线l和直线BH相交于点M,当点B在圆上运动时,点M的轨迹记为曲线C.(1)求C的方程;
(2)设直线m与曲线C交于P,Q两点,O为坐标原点,若∠POQ=90°,问$\frac{1}{|OP{|}^{2}}$+$\frac{1}{|OQ{|}^{2}}$是否为定值?若是求其定值,若不是说明理由.
分析 (1)由圆的方程求出圆心坐标和半径,由|MA|+|MH|=|MB|+|MH|=|BH|=4可得点M的轨迹是以A,H为焦点,4为长轴长的椭圆,则其标准方程可求;
(2)分类讨论,设直线OP方程为y=kx(k≠0),与椭圆方程联立可得x2,y2.进而得到|OP|2,同理得到|OQ|2,即可证明为定值.
解答 解:(1)由x2+y2+2x-15=0,得(x+1)2+y2=42,
∴圆心为H(-1,0),半径为4,
连接MA,由l是线段AB的中垂线,得|MA|=|MB|,
∴|MA|+|MH|=|MB|+|MH|=|BH|=4,
又|AH|=2<4,
故点M的轨迹是以A,H为焦点,4为长轴长的椭圆,其方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1;
(2)设直线OP方程为y=kx(k≠0),联立椭圆方程,解得${x}^{2}=\frac{12}{3+4{k}^{2}},y=\frac{12{k}^{2}}{3+4{k}^{2}}$,
∴|OP|2=$\frac{12({k}^{2}+1)}{3+4{k}^{2}}$.
同理解得|OQ|2=$\frac{12({k}^{2}+1)}{4+3{k}^{2}}$.
∴$\frac{1}{|OP{|}^{2}}$+$\frac{1}{|OQ{|}^{2}}$=$\frac{7}{12}$,
OP斜率不存在时,|OP|2=3,|OQ|2=4,$\frac{1}{|OP{|}^{2}}$+$\frac{1}{|OQ{|}^{2}}$=$\frac{7}{12}$
综上所述,$\frac{1}{|OP{|}^{2}}$+$\frac{1}{|OQ{|}^{2}}$=$\frac{7}{12}$是定值.
点评 本题考查椭圆标准方程的求法,考查了直线与椭圆位置关系的应用,考查学生的计算能力,属中档题.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案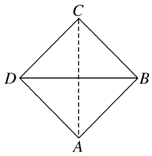 已知正四面体(所有棱长都相等的三棱锥)的俯视图如图所示,其中四边形ABCD是边长为$\sqrt{2}$cm的正方形,则这个正四面体的主视图的面积为( )cm2.
已知正四面体(所有棱长都相等的三棱锥)的俯视图如图所示,其中四边形ABCD是边长为$\sqrt{2}$cm的正方形,则这个正四面体的主视图的面积为( )cm2.| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
| A. | 2 | B. | 3 | C. | 2$\sqrt{2}$ | D. | 2.5 |
| A. | m>9 | B. | m≥9 | C. | m≥7 | D. | m>7 |
