题目内容
已知函数f(x)=
,若对任意的a∈(-3,+∞),关于x的方程f(x)=kx都有3个不同的根,则k等于( )
|
| A、1 | B、2 | C、3 | D、4 |
考点:分段函数的应用
专题:函数的性质及应用
分析:根据a取值的任意性,利用特殊值法,结合数形结合即可得到结论.
解答:
解:∵对任意的a∈(-3,+∞),关于x的方程f(x)=kx都有3个不同的根,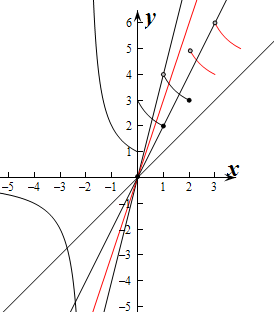
∴不妨设a=0,
则x≤0时,f(x)=
,
若0<x≤1,则-1<x-1≤0,则f(x)=f(x-1)+1=
+1,
若1<x≤2,则0<x-1≤1,则f(x)=f(x-1)+1=
+2,
若2<x≤3,则1<x-1≤2,则f(x)=f(x-1)+1=
+3,
若3<x≤4,则2<x-1≤3,则f(x)=f(x-1)+1=
+4,
…
作出f(x)的图象如图:
当k=1时,f(x)与y=x只有一个交点,不满足条件,
当k=2时,f(x)与y=2x有四个交点,不满足条件,
当k=3时,f(x)与y=3x有三个交点,满足条件,
当k=4时,f(x)与y=4x只有两个交点,不满足条件,
故k=3,
故选:C.

∴不妨设a=0,
则x≤0时,f(x)=
| 2 |
| x+2 |
若0<x≤1,则-1<x-1≤0,则f(x)=f(x-1)+1=
| 2 |
| x+1 |
若1<x≤2,则0<x-1≤1,则f(x)=f(x-1)+1=
| 2 |
| x |
若2<x≤3,则1<x-1≤2,则f(x)=f(x-1)+1=
| 2 |
| x-1 |
若3<x≤4,则2<x-1≤3,则f(x)=f(x-1)+1=
| 2 |
| x-2 |
…
作出f(x)的图象如图:
当k=1时,f(x)与y=x只有一个交点,不满足条件,
当k=2时,f(x)与y=2x有四个交点,不满足条件,
当k=3时,f(x)与y=3x有三个交点,满足条件,
当k=4时,f(x)与y=4x只有两个交点,不满足条件,
故k=3,
故选:C.
点评:本题主要考查方程根的个数的应用,利用数形结合以及特殊值法是解决本题的关键.本题综合性较强,难度较大,如果正面求解,一般无法寻找突破口.

练习册系列答案
相关题目
已知0<a<b,a+b=1,则
,b,a2+b2的大小关系是( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、a2+b2<b<
| ||
| D、无法确定 |
下列各函数中,最小值为2的是( )
| A、y=log2x+logx2 | ||||
| B、y=2x+2-x | ||||
C、y=
| ||||
D、y=x+
|
已知函数f(x)满足:①当0≤x≤2时,f(x)=(x-1)2,②?x∈[0,8],f(x-
)=f(x+
).若方程f(x)=Mlog2x在[0,8]上有偶数个根,则正数M的取值范围是( )
| 1 |
| 2 |
| 3 |
| 2 |
A、0<M≤
| ||||
B、0<M≤
| ||||
C、0<M≤
| ||||
D、0<M≤
|
若函数y=sinωx(ω>0)的图象向左平移
个单位后与原图象重合,则ω的最小值是( )
| 4π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知a>2,b>2,则( )
| A、ab≥a+b |
| B、ab≤a+b |
| C、ab>a+b |
| D、ab<a+b |
定义:设f″(x)是函数y=f(x)的导函数y=f′(x)的导数,若f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.现已知f(x)=x3-3x2+2x-2,则函数y=f(x)的“拐点”A的坐标为( )
| A、(-1,-8) |
| B、(0,-2) |
| C、(1,-2) |
| D、(2,-10) |